Урок 103
Основы растровой графики
(§56. Основы растровой графики)
Содержание урока
Что такое разрешение?
Что такое разрешение?
Как вы знаете из курса 10 класса, растровый рисунок, как мозаика, состоит из отдельных «квадратиков»-пикселей, каждый из которых закрашен своим цветом. Цвет кодируется как набор чисел, например в модели RGВ цвет пикселя задаётся тремя значениями — красной (англ. R — red), зелёной (англ. G — green) и синей (англ. В — blue) составляющими.
В этой главе вы узнаете о том, как можно обрабатывать растровые изображения с помощью современных графических редакторов.
Любое изображение, в конечном счёте, предназначено для просмотра. При выводе на экран или на печать оно должно иметь определённые размеры, поэтому нужно установить связь между шириной и высотой рисунка в пикселях и его размерами (в сантиметрах или других единицах длины) на экране монитора или на бумаге. Эту связь определяет разрешение, т. е. число пикселей на некотором отрезке изображения (по ширине или высоте). По традиции разрешение измеряется в пикселях на дюйм 1 (англ. ppi — pixels per inch). Чем больше разрешение, тем выше качество изображения, но тем больше места оно занимает в памяти.
1 1 дюйм = 2,54 см.
Например, пусть мы хотим вывести на экран изображение размером 10 х 15 см. Каковы будут размеры рисунка в пикселях? Обычно стандартным разрешением для изображения на экране считается 2 72 ppi или 96 ppi. При разрешении 96 ppi размеры рисунка в пикселях должны быть равны:
высота: 10 • 96 / 2,54 ≈ 378 пикселей;
ширина: 15 • 96 / 2,54 ≈ 567 пикселей.
2 Разрешение 96 ppi, например, соответствует размерам экрана 1280 х 1024 пикселя для монитора с диагональю 17 дюймов.
Конечно, нужно учитывать, что фактическое разрешение экрана может отличаться от 96 ppi, оно зависит от размера монитора и режима работы видеокарты (заданного в её настройках количества пикселей по ширине и высоте экрана).
Теперь предположим, что нам нужно напечатать на бумаге стандартную фотокарточку того же размера (10 х 15 см). Печатающие устройства могут обеспечить значительно более высокое разрешение, чем экран. Для получения отпечатков среднего качества (при котором уже практически незаметно, что изображение состоит из пикселей) требуется разрешение около 300 ppi, а для профессиональных работ — 600 ppi и более (до 2400 ppi). При разрешении 300 ppi размеры рисунка в пикселях будут совсем другие:
высота: 10 • 300 / 2,54 ≈ 1181 пиксель;
ширина: 15 • 300 / 2,54 ≈ 1772 пикселя.
На рисунке 8.1 для сравнения показано одно и то же изображение с разным разрешением.

Рис. 8.1
Заметно, что изображение с разрешением 300 ppi смотрится вполне естественно (пиксели не видны), а при разрешении 24 ppi ромашки уже с трудом угадываются в получившемся наборе пикселей.
Для иллюстрации мы будем использовать свободный растровый графический редактор GIMP (www.gimp.org), версии которого существуют для Windows, Linux и Mac OS. Другие популярные редакторы, например Adobe Photoshop, имеют аналогичные возможности.
Если в редактор GIMP загрузить некоторое изображение, с помощью меню Изображение — Размер изображения можно посмотреть и изменить его параметры (рис. 8.2).
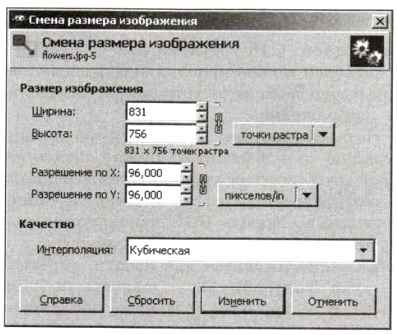
Рис. 8.2
По умолчанию размер изображения задаётся в пикселях (точках растра). Чтобы увидеть размеры отпечатка (в сантиметрах или миллиметрах), в выпадающем списке справа нужно выбрать соответствующую единицу измерения.
Это диалоговое окно позволяет также менять размеры рисунка и его разрешение. Изменяя размер изображения в пикселях, мы искажаем рисунок. Например, пусть при увеличении размера нужно заменить 5 пикселей на 8. В этом случае программе приходится с помощью математических методов перестроить картинку так, чтобы изображение сохранилось как можно лучше. Алгоритм такой обработки задаётся в поле Интерполяция 3. Кубическая интерполяция считается одной из лучших, однако при использовании этого метода изображение немного размывается. Чтобы сохранить чёткие границы на рисунке, в списке Интерполяция нужно выбрать вариант Никакая.
При изменении разрешения количество пикселей в рисунке остаётся тем же, поэтому никакой потери качества не происходит. Однако размеры отпечатка изменятся: если увеличить разрешение, при печати изображение уменьшится.
3 Интерполяция — это восстановление промежуточных значений функции.
Следующая страница  Цветовые модели
Цветовые модели

