Первая задача не имеет строгого решения. Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.

Чаще всего выбор производится среди следующих функций:

у = ах + b — линейная функция;
у = ах² + bх + с — квадратичная функция;
у = а lп(х) + b — логарифмическая функция;
у = ае^bх — экспоненциальная функция;
у = ах^b — степенная функция.

Квадратичная функция называется в математике полиномом второй степени. Иногда используются полиномы и более высоких степеней, например полином третьей степени имеет вид:

у = ах³ + bх² + сх + d.

Во всех этих формулах х — аргумент, у — значение функции, а, b, с, d — параметры функции, lп(х) — натуральный логарифм, е — константа, основание натурального логарифма.

Если вы выбрали (сознательно или наугад) одну из предлагаемых функций, то далее нужно подобрать параметры (а, Ь, с и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Что значит «располагалась как можно ближе»? Ответить на этот вопрос значит предложить метод вычисления параметров. Такой метод был предложен в XVIII веке немецким математиком К. Гауссом и называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.

Мы не будем здесь производить подробное математическое описание метода наименьших квадратов. Достаточно того, что вы теперь знаете о существовании такого метода. Он очень широко используется в статистической обработке данных и встроен во многие математические пакеты программ. Важно понимать следующее: методом наименьших квадратов по данному набору экспериментальных точек можно построить любую (в том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлетворять, это уже другой вопрос — вопрос критерия соответствия. На рис. 3.5 изображены три функции, построенные методом наименьших квадратов по приведенным экспериментальным данным.

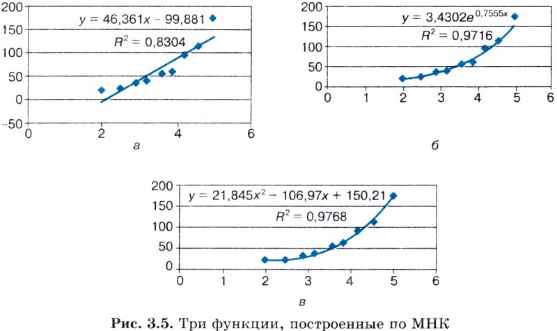
Эти рисунки получены с помощью табличного процессора Microsoft Excel. График регрессионной модели называется трендом. Английское слово trend можно перевести как «общее направление» или «тенденция».

Уже с первого взгляда хочется отбраковать вариант линейного тренда. График линейной функции — это прямая. Полученная по МНК прямая отражает факт роста заболеваемости от концентрации угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды правдоподобны. Теперь пора обратить внимание на надписи, присутствующие на графиках.

Во-первых, это записанные в явном виде искомые функции — регрессионные модели:

линейная функция: у = 46,361x - 99,881;
экспоненциальная функция: у = 3,4302 е^0,7555х;
квадратичная функция: у = 21,845x² -106,97х + 150,21.

На графиках присутствует еще одна величина, полученная в результате построения трендов. Она обозначена как R². В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной является полученная регрессионная модель. Коэффициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели предельно неудачен. Чем R² ближе к 1, тем удачнее регрессионная модель.

Из трех выбранных моделей значение R² наименьшее у линейной. Значит, она самая неудачная (нам и так это было понятно). Значения же R² у двух других моделей достаточно близки (разница меньше 0,01). Если определить погрешность решения данной задачи как 0,01, по критерию R² эти модели нельзя разделить. Они одинаково удачны. Здесь могут вступить в силу качественные соображения. Например, если считать, что наиболее существенно влияние концентрации угарного газа проявляется при больших величинах, то, глядя на графики, предпочтение следует отдать квадратичной модели. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.

Интересный факт: опыт показывает, что если человеку предложить на данной точечной диаграмме провести «на глаз» прямую так, чтобы точки были равномерно разбросаны вокруг нее, то он проведет линию, достаточно близкую к той, что дает МНК.

Следующая страница Прогнозирование по регрессионной модели

Уроки 21 - 32Модели статистического прогнозирования (§18)Практическая работа № 3.2. "Прогнозирование"

Содержание урока

Модели статистического прогнозирования (§18)

Метод наименьших квадратов

Уроки 21 - 32
Модели статистического прогнозирования (§18)
Практическая работа № 3.2. "Прогнозирование"