Цель работы: освоение приемов прогнозирования количественных характеристик системы по регрессионной модели путем восстановления значений и экстраполяции.

Используемое программное обеспечение: табличный процессор Microsoft Excel.

Задание 1

Требуется выполнить прогнозирование заболеваемости бронхиальной астмой при концентрации угарного газа 3 мг/куб. м методом восстановления значения, воспользовавшись квадратичной зависимостью, полученной в предыдущей работе.

1. Построить следующую электронную таблицу:

2. Подставить в ячейку А2 значение концентрации угарного газа, равное 3 мг/куб. м. В результате получим:

Справочная информация

Число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена — в формате вывода числа указано 0 цифр после запятой.

Задание 2

Требуется выполнить прогнозирование заболеваемости бронхиальной астмой при концентрации угарного газа б мг/куб. м методом графической экстраполяции, воспользовавшись квадратичной зависимостью, полученной в предыдущей работе.

1. Выполнить построение квадратичного тренда по алгоритму, описанному в предыдущей работе, добавив в него следующее действие:

=> на вкладке Параметры в области Прогноз в строке вперед на установить 2 единицы.

Здесь имеются в виду единицы используемого масштаба по горизонтальной оси.

Полученный график приведен на рисунке.

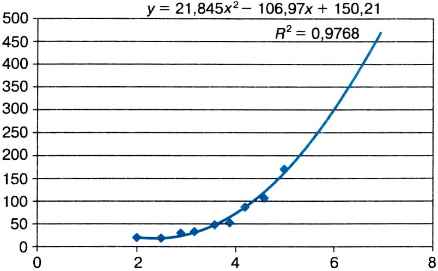
2. Оценить приблизительно на полученном графике значение функции при значении аргумента, равном 6.

Следующая страница Моделирование корреляционных зависимостей (§19)

Уроки 21 - 32Модели статистического прогнозирования (§18)Практическая работа № 3.2. "Прогнозирование"

Содержание урока

Модели статистического прогнозирования (§18)

ПрактикумПрактическая работа № 3.2Прогнозирование

Задание 1

Задание 2

Уроки 21 - 32
Модели статистического прогнозирования (§18)
Практическая работа № 3.2. "Прогнозирование"

Практикум
Практическая работа № 3.2
Прогнозирование