Уроки 21 - 32
Модели оптимального планирования (§20)
Практическая работа № 3.6. "Решение задачи оптимального планирования
Содержание урока
Компьютерное информационное моделирование (§16)
Моделирование зависимостей между величинами (§17)
Модели статистического прогнозирования (§18)
Моделирование корреляционных зависимостей (§19)
Модели оптимального планирования (§20)
Целевая функция
Практическая работа № 3.6 Решение задачи оптимального планирования
Итоговое тестирование по теме "Информационное моделирование"
Модели оптимального планирования (§20)
Целевая функция
А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна
rх + 2rу = r(х + 2у).
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
F(x, у) = r(х + 2у).
Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять
f(x, у) = х + 2у. (2)
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2).
Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.
Теперь следующий вопрос: как решить эту задачу? Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода.
Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию f(x, у) величины хну входят линейно (т. е. в первой степени), наша задача относится к разделу этой науки, который называется линейным программированием.
Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:
х + 4у = 1000,
х + у = 700,
х = 0 (ось У).
у = 0 (ось X)
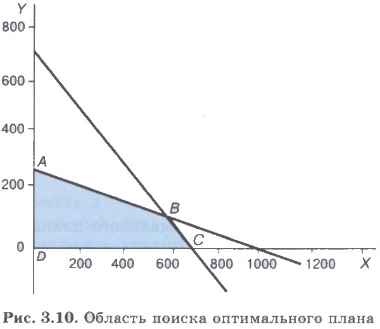
На рис. 3.10 эта область представляет собой четырехугольник ABCD и выделена заливкой. Любая точка четырехугольника является решением системы неравенств (1). Например, х = 200, у = 100. Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке (x = 600, у = 50) соответствует f(600, 50) = 700. Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.
В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума.
В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис. 3.10. В этой точке значение целевой функции f(600, 100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.

Вопросы и задания
1.
а) В чем состоит задача оптимального планирования?
б) Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.
2.
а) Попробуйте сформулировать содержание оптимального планирования для своей учебной деятельности.
б) Что такое математическое программирование, линейное программирование?
3.
а) Сформулируйте задачу оптимального планирования для школьного кондитерского цеха, в котором выпускается три вида продукции: пирожки, пирожные и коржики.
б) Внесите изменение в постановку задачи оптимального планирования из этого параграфа для двух видов продукции с учетом еще одного ограничения: число пирожных должно быть не меньше числа пирожков. На координатной плоскости постройте область поиска решения.
Следующая страница  Вопросы и задания
Вопросы и задания

