Уроки 2 - 3
Информация и вероятность. Формула Хартли. Формула Шеннона
(§1. Количество информации)
Содержание урока
Формула Шеннона
Формула Шеннона

Информация играет для нас важную роль потому, что наше знание всегда неполно, в нём есть неопределенность. Эта неопределённость мешает нам решать свои задачи, принимать правильные решения. Полученная информация уменьшает («снимает») неопределённость, полностью или частично. Поэтому количество полученной информации можно оценить по величине уменьшения неопределенности:
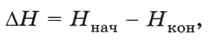
где ННАЧ — начальная неопределённость, а НКОН — конечная (после получения сообщения).
Если неопределённость полностью снимается, то НКОН = 0.
Чтобы оценить информацию с этой точки зрения, нужно как-то вычислить неопределённость, выразить её числом. Эту задачу решил в 1948 г. американский математик Клод Шеннон.
Пусть неопределённость состоит в том, что мы можем получить одно из N возможных сообщений, причём известно, что вероятность получения сообщения с номером i равна рi.
Неопределённость знания об источнике данных вычисляется по формуле Шеннона
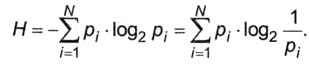
Величина Н часто называется информационной энтропией. С точки зрения математики это среднее количество информации, которую мы получаем при полном снятии неопределённости (когда выбран один из возможных вариантов).
Когда неопределённость наибольшая? Зададим вопрос «Идёт ли сейчас снег?» зимой и летом. Летом неопределённость очень маленькая, так как, скорее всего, снега нет, ситуация ясна. Зимой же неопределённость велика, потому что снег может идти или не идти примерно с равной вероятностью.
Перейдём к числам. Будем считать, что вероятность снега зимой равна P1 = 0,5. Чему равна вероятность р2 того, что снега нет? «Здравый смысл» подсказывает, что р2 = 0,5 (остальные 50%). Математики говорят, что два события, «Снег идёт» и «Снега нет», составляют полную систему. Это значит, что обязательно случится какое-нибудь одно из этих событий, и при этом другое точно не произойдёт. Слово «обязательно» означает, что вероятность этих двух событий в сумме равна 1.
Сумма вероятностей всех событий, составляющих полную систему, равна 1.
Для «зимнего» случая количество информации при получении сообщений «Снег идёт» и «Снега нет» одинаковое, потому что их вероятности одинаковые:
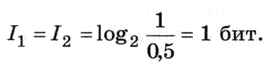
Неопределённость, вычисленная по формуле Шеннона, также равна 1 биту:
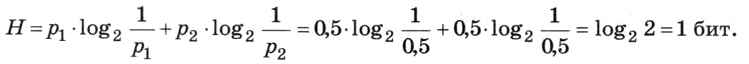
Для лета будем считать вероятность выпадения снега равной р1 = 0,0001. Тогда вероятность того, что снега нет, равна р2 = 1 - 0,0001 = 0,9999. Сообщения «Снег идёт» и «Снега нет» несут разное количество информации:
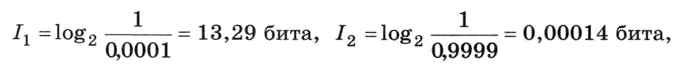
а неопределённость (среднее количество информации) равна

Мы получили то, что ожидали: зимой неопределённость в ответе на вопрос «Идёт ли сейчас снег?» значительно больше, чем летом. Можно предположить (и это действительно так), что неопределённость наибольшая в том случае, когда вероятности всех событий равны.
Летом эта неопределённость очень близка к нулю, поэтому можно предположить (и это также верно), что она стремится к нулю, если вероятность одного из двух событий стремится к нулю.
На рисунке 1.1 построена зависимость величины неопределённое Н от вероятности первого события p1. При этом вероятность второго события определяется как р2 = 1 - p1, так как они составляют полную систему. Главный вывод этого примера таков:
 Неопределённость наибольшая для случая, когда все события равновероятны.
Неопределённость наибольшая для случая, когда все события равновероятны.
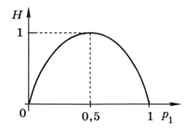
Рис. 1.1
При этом вероятность каждого из N событий равна р = 1/N, поэтому по формуле Шеннона
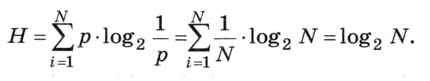
Отсюда следует, что:
 При равновероятных событиях неопределённость совпадает с количеством информации, вычисленной по формуле Хартли.
При равновероятных событиях неопределённость совпадает с количеством информации, вычисленной по формуле Хартли.
Следующая страница  Вопросы и задания
Вопросы и задания

