Уроки 6 - 7
Сжатие данных без потерь
(§3. Сжатие данных)
Содержание урока
Алгоритм Хаффмана
Алгоритм Хаффмана
Было доказано, что в некоторых случаях кодирование Шеннона-Фано дает неоптимальное решение, и можно построить код, который ещё больше уменьшит длину кодовой последовательности. Например, в предыдущем примере (код Шеннона-Фано) пробел и буква «Т» имеют коды одинаковой длины, хотя буква «Т» встречается в 3,5 раза реже пробела. Через несколько лет Дэвид Хаффман, ученик Фано, разработал новый алгоритм кодирования и доказал его оптимальность.

Построим код Хаффмана для того же самого примера. Сначала отсортируем буквы по увеличению частоты встречаемости:

Затем берём две самые первые буквы, они становятся листьями дерева, а в узел, с которым они связаны, записываем сумму их частот:
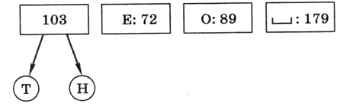
Таким образом, буквы, которые встречаются реже всего, получили самый длинный код. Снова сортируем буквы по возрастанию частоты, но для букв «Т» и «Н» используется их суммарная частота:
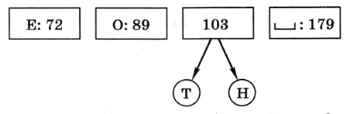
Повторяем ту же процедуру для букв «Е» и «О», частоты которых оказались минимальными, и сортируем по возрастанию частоты:
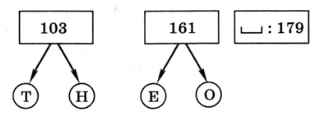
Теперь объединяем уже не отдельные буквы, а пары, и снова сортируем
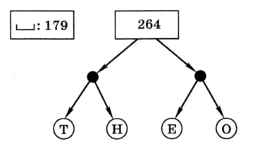
На последнем шаге остаётся объединить символ «пробел» с деревом, которое построено для остальных символов. У каждой стрелки, идущей влево от какого-то узла, ставим код 0, а у каждой стрелки, идущей вправо — код 1 (рис. 1.4).
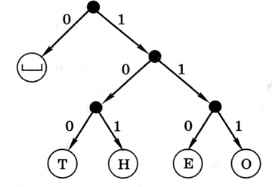
Рис. 1.4
По этому дереву, спускаясь от корня к листьям-символам, получаем коды Хаффмана, обеспечивающие оптимальное сжатие с учётом частоты встречаемости символов:
 — О, Т — 100, О — 111, Е — 110, Н — 101.
— О, Т — 100, О — 111, Е — 110, Н — 101.
Легко проверить, что этот код также удовлетворяет условию Фано.
Сравним эффективность рассмотренных выше методов. Для алфавита из 5 символов при равномерном кодировании нужно использовать 3 бита на каждый символ, так что общее число битов в сообщении равно (179 + 89 + 72 + 53 + 50) • 3 = 1329 битов. При кодировании методом Шеннона-Фано получаем 179 • 2 + 89 • 2 + 72 • 3 + 53 • 3 + 50 • 2 = 1011 битов, коэффициент сжатия составляет 1329/1011 ≈ 1,31. Использование кода Хаффмана даёт последовательность длиной 179 • 1 + 89 • 3 + 72 • 3 + 53 • 3 + 50 • 3 = 971 бит, коэффициент сжатия равен 1,37. В сравнении со случаем, когда для передачи используется однобайтный код (8 битов на символ), выигрыш получается ещё более весомым: кодирование Хаффмана сжимает данные примерно в 3,65 раза. Обратим внимание, что сжать данные удалось за счёт избыточности: мы использовали тот факт, что некоторые символы встречаются чаще, а некоторые — реже.
Алгоритм кодирования Хаффмана и сейчас широко применяется благодаря своей простоте, высокой скорости кодирования и отсутствию патентных ограничений (он может быть использован свободно). Например, он применяется на некоторых этапах при сжатии рисунков (в формате JPEG) и звуковой информации (в формате MP3).
Следующая страница  Сжатие с потерями
Сжатие с потерями

