Уроки 19 - 20
Системы массового обслуживания
(§11. Системы массового обслуживания)
Содержание урока
Что такое системы массового обслуживания?
Модель обслуживания в банке
Модель обслуживания в банке
Рассмотрим достаточно простую модель работы банка. Клиенты входят через случайные промежутки времени, их обслуживают несколько кассиров, причём время обслуживания - также случайная величина. Требуется определить, сколько кассиров нужно для того, чтобы клиент стоял в очереди не более М минут.
В таком виде задача некорректна (плохо поставлена) — неясно, как определить длину очереди. Поэтому нужно вводить допущения, которые позволят сделать задачу хорошо поставленной и решить её.
Сначала построим детерминированную модель, в которой случайность не учитывается. Будем считать, что за 1 минуту входит ровно Р клиентов, причём каждый клиент обслуживается ровно Т минут.
Если количество касс равно К, за Т минут будет обслужено ровно К клиентов. За это же время в банк войдут Р • Т новых клиентов. Несложно понять, что если К < Р • Т, клиенты входят быстрее, чем их успевают обслуживать, поэтому очередь будет постоянно расти. Если же К ≥ Р • Т, очереди вообще не будет, из этого условия и нужно выбирать количество касс. Например, при Р = 2 и Т = 5 для обслуживания нужно не менее 10 касс.
Теперь усложним модель: введем в неё случайные события.
ТБудем считать, что:
• за 1 минуту в банк входит случайное число клиентов, от 0 до Pmах;
• на обслуживание клиентов требуется от Tmin до Тmах минут.
Для моделирования нужно ещё определить, как распределены случайные данные (количество входящих за 1 минуту и время обслуживания) внутри заданных интервалов. Для простоты мы будем считать, что в обоих случаях распределение равномерное. Тогда можно применить стандартные генераторы случайных чисел, которые дают именно равномерно распределённые значения.
Будем использовать имитационную модель — выполним моделирование ситуации для достаточно большого интервала времени L (например, для 8-часового рабочего дня L = 8 • 60 = 480 минут).
Число клиентов, находящихся в помещении банка, изменяется по закону:
Ni+1 = Ni + Pi — Ri,
где Pi — количество клиентов, вошедших за i-ю минуту, a Ri — количество клиентов, обслуженных за это время. Считаем, что N клиентов равномерно распределяются по К кассам, так что средняя длина очереди равна Q = N/K, а среднее время ожидания равно Q • Т.
Количество вошедших Рi — это случайное целое число в интервале от 0 до Рmах. На школьном алгоритмическом языке и на Паскале его можно получить так:
P:=irand(0,РМах) P:=random(РМах + 1);
Определить число обслуженных Ri оказывается не так просто. Если кассир обслуживает клиента за Т минут, то можно считать, что за 1 минуту он сделает часть работы, равную 1/T. Если предположить, что скорость работы кассиров одинакова, то К касс за 1 минуту обслужат 1/K клиентов. Чтобы учесть случайное время обслуживания, величину Т будем определять заново для каждой минуты случайным образом. Это случайное вещественное число в интервале от Tmin до Тmах:
T:=rand(Tmin,Tmax) T:=Tmin+random*(Tmax-Tmin);
Тогда можно рассчитать значение среднего времени ожидания по формуле
Это значение будет меняться, поскольку N и Т — случайные величины. Именно поэтому невозможно гарантировать, что клиент точно не будет ждать больше положенного времени М. Вместо этого мы можем (с помощью имитационного моделирования) подсчитать, какую долю времени оценка интервала ожидания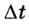 
будет больше, чем М минут. Для определения этой доли нужно подсчитать количество «плохих» минут и разделить его на общее время моделирования L.
Если доля «плохого» времени получилась, например, 0,95 (95%), то клиент практически всегда вынужден будет ждать слишком долго, и количество касс нужно увеличивать. Если эта доля равна 0,05, то время ожидания будет больше допустимого только в 5% случаев, такой результат можно считать приемлемым.
Таким образом, нужно составить программу, которая запрашивает количество касс, выполняет моделирование работы банка в течение рабочего дня и выдает долю «плохих» минут. Сначала задаём начальные значения переменных:
Затем нужно ввести количество кассиров К. Основной цикл моделирует работу банка в течение L минут:
На каждом шаге последовательно вычисляются:
• случайное число входящих клиентов Р;
• случайное время обслуживания Т;
• число клиентов R, обслуженных за эту минуту;
• число клиентов в помещении банка N; если оно получилось отрицательным, то используется нулевое значение;
• время ожидания; если оно больше допустимого времени М, увеличивается счетчик «плохих» минут.
После окончания работы цикла остаётся вывести результат — отношение count/L, которое представляет собой долю «плохих» минут. Нужно провести серию экспериментов с моделью и выбрать минимальное значение К, при котором доля «плохих» минут будет менее 5%. Помните, что в модели используются случайные числа, поэтому при каждом новом запуске программы результаты расчётов будут немного меняться. Теперь вы можете написать полную программу и найти с её помощью нужное число касс.
Обратите внимание, что мы выбрали исходные данные так, чтобы среднее число входящих клиентов и среднее время обслуживания совпадали с теми же данными для детерминированной модели. Поэтому интересно сравнить результаты, полученные с помощью моделей двух типов: детерминированной и вероятностной. Скорее всего, они окажутся близкими, хотя и будут немного различаться. Тогда возникает вопрос: какая модель даёт более точный результат? Ответить на него можно только с помощью эксперимента, проведённого в реальном банке.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
