Уроки 43 - 44
Стек, очередь, дек
(§42. Стек, очередь, дек)

Содержание урока

Что такое стек?

Использование динамического массива

Вычисление арифметических выражений

Скобочные выражения

Очереди, деки

Вопросы и задания

Задачи

Очереди, деки

Все мы знакомы с принципом очереди: первый пришёл — первый обслужен (англ. FIFO: First In — First Out). Соответствующая структура данных в информатике тоже называется очередью .

Очередь — это линейный список, для которого введены две операции:

• добавление нового элемента в конец очереди;
• удаление первого элемента из очереди.

Очередь — это не просто теоретическая модель. Операционные системы используют очереди для организации сообщений между программами: каждая программа имеет свою очередь сообщений. Контроллеры жёстких дисков формируют очереди запросов ввода и вывода данных. В сетевых маршрутизаторах создаётся очередь из пакетов данных, ожидающих отправки.

Задача 3. Рисунок задан в виде матрицы А, в которой элемент А[y, х] определяет цвет пикселя (х, y) на пересечении строки y и столбца х. Требуется перекрасить в цвет 2 одноцветную область, начиная с пикселя (х₀, y₀). На рисунке 6.9 показан результат такой заливки для матрицы из 5 строк и 5 столбцов с начальной точкой (2,1).

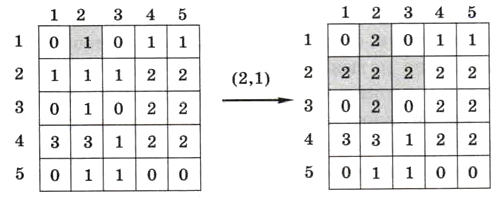
Рис. 6.9

Эта задача актуальна для графических программ. Один из возможных вариантов решения использует очередь, элементы которой — координаты пикселей (точек):

добавить в очередь точку (х0,y0) 
запомнить цвет начальной точки 
нц пока очередь не пуста
	взять из очереди точку (х,y) 
	если А[y,х]=цвету начальной точки то
		А[y,х]:=2;
		добавить в очередь точку (х-1,y) 
		добавить в очередь точку (х+1,y) 
		добавить в очередь точку (х,y-1) 
		добавить в очередь точку (х,y+1) 
	все
кц

Конечно, в очередь добавляются только те точки, которые находятся в пределах рисунка (матрицы А). Заметим, что в этом алгоритме некоторые точки могут быть добавлены в очередь несколько раз (подумайте, когда это может случиться). Поэтому алгоритм можно несколько улучшить, как-то помечая точки, уже добавленные в очередь, чтобы не добавлять их повторно (попробуйте сделать это самостоятельно).

Две координаты точки связаны между собой, поэтому в программе лучше объединить их в структуру TPoint (от англ. point — точка), а очередь составить из таких структур:

Type TPoint = record 
		х, y: integer; 
	end;
	TQueue = record
		data: array of TPoint; 
		size: integer 
	end;

Для удобства построим функцию Point, которая формирует структуру типа TPoint по заданным координатам:

function Point(x,y: integer): TPoint;
begin
	Point.x:=x;
	Point.y:=y 
end;

Для работы с очередью, основанной на динамическом массиве, введём две подпрограммы:

• процедура Put добавляет новый элемент в конец очереди; если нужно, массив расширяется блоками по 10 элементов;
• функция Get возвращает первый элемент очереди и удаляет его из очереди (обработку ошибки «очередь пуста» вы можете сделать самостоятельно); все следующие элементы сдвигаются к началу массива.

procedure Put(var Q: TQueue; pt: TPoint); 
begin
	if Q.size > High(Q.data) then
		SetLength(Q.data, Length(Q.data)+10);
	Q.data[Q.size]:=pt;
	Q.size:=Q.size+1 
end;
function Get(var Q:TQueue): TPoint;
var i: integer;
begin
	Get:=Q.data[0];
	Q. size:=Q.size-1; 
	for i:=0 to Q.Size-1 do 
		Q.data[i]:=Q.data[i+1]
end;

Остаётся написать основную программу. Объявляем константы и переменные:

const ХМАХ = 5; YМАХ = 5;
      NEW_COLOR = 2; 
var Q: TQueue;
	x0, yO, color: integer;
	A: array[1..УМАХ,1..XMAX] of integer; 
	pt: TPoint;

Предположим, что матрица А заполнена. Задаём исходную точку, с которой начинается заливка, запоминаем её «старый» цвет и добавляем эту точку в очередь:

х0:=2; y0:=1; 
color:=А[у0,х0];
Put (Q, Point (х0, y0) ) ;

Основной цикл практически повторяет алгоритм на псевдокоде:

while not isEmpty(Q) do begin 
	pt:=Get(Q);
	if A[pt.y,pt.x]=color then begin 
		A[pt.y,pt.x]:=NEW_COLOR;
		if pt.x>1 then Put(Q,Point(pt.x-1,pt.y)); 
		if pt.x<XMAX then Put(Q,Point(pt.x+1,pt.y)); 
		if pt.y>1 then Put(Q,Point(pt.x,pt.y-1)); 
		if pt.y<YMAX then Put(Q,Point(pt.x,pt.y+1)) 
	end 
end;

Здесь функция isEmpty — такая же, как и для стека: возвращает True, если очередь пуста (поле size равно нулю).

В приведённом примере начало очереди всегда совпадает с первым элементом массива (имеющим индекс 0). При этом удаление элемента из очереди неэффективно, потому что требуется сдвинуть все оставшиеся элементы к началу массива. Существует и другой подход, при котором элементы очереди не передвигаются. Допустим, что мы знаем, что количество элементов в очереди всегда меньше N. Тогда можно выделить статический массив из N элементов (с индексами от 1 до N) и хранить в отдельных переменных номера первого элемента очереди («головы», англ. head) и последнего элемента («хвоста», англ. tail). На рисунке 6.10, а показана очередь из 5 элементов. В этом случае удаление элемента из очереди сводится просто к увеличению переменной Head (рис. 6,10, б).

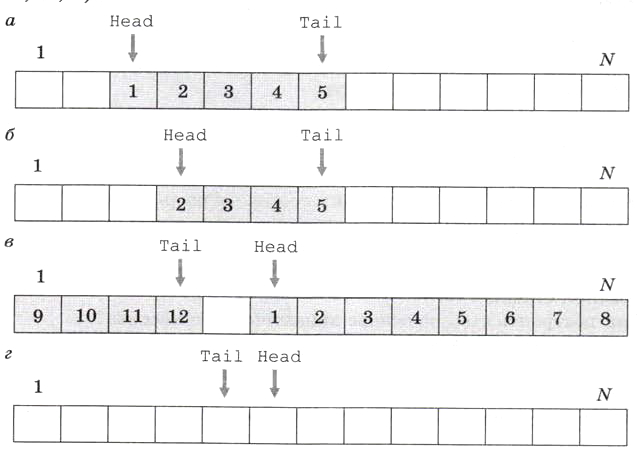
Рис. 6.10

При добавлении элемента в конец очереди переменная Tail увеличивается на 1. Если она перед этим указывала на последний элемент массива, то следующий элемент записывается в начало массива, а переменной Tail присваивается значение 1. Таким образом, массив оказывается замкнутым «в кольцо». На рисунке 6.10, в показана целиком заполненная очередь, а на рис. 6.10, г — пустая очередь. Один элемент массива всегда остаётся незанятым, иначе невозможно будет различить состояния «очередь пуста» и «очередь заполнена».

Отметим, что приведённая здесь модель описывает работу кольцевого буфера клавиатуры, который может хранить до 15 двухбайтных слов.

Кроме того, очередь можно построить на основе связного списка (см. § 41). Детали такой реализации можно найти в литературе или в Интернете.

Существует еще одна линейная динамическая структура данных, которая называется дек.

Дек — это линейный список, в котором можно добавлять и удалять элементы как с одного, так и с другого конца.

Из этого определения следует, что дек может работать и как стек, и как очередь. С помощью дека можно, например, моделировать колоду игральных карт

Следующая страница Вопросы и задания

Cкачать материалы урока