Уроки 45 - 46
Деревья. Основные понятия
(§43. Деревья)
Содержание урока
Что такое дерево?
Вычисление арифметических выражений
Использование связанных структур
Хранение двоичного дерева в массиве
Что такое дерево?
Как вы знаете из учебника 10 класса, дерево — это структура, отражающая иерархию (отношения подчинённости, многоуровневые связи). Напомним некоторые основные понятия, связанные с деревьями.
Дерево состоит из узлов и связей между ними (они называются дугами). Самый первый узел, расположенный на верхнем уровне (в него не входит ни одна стрелка-дуга), — это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, — это промежуточные узлы.
Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой — сыном. Корень — это единственный узел, у которого нет родителя; у листьев нет сыновей.
Используются также понятия «предок» и «потомок». Потомок какого-то узла — это узел, в который можно перейти по стрелкам от узла-предка. Соответственно, предок какого-то узла — это узел, из которого можно перейти по стрелкам в данный узел.
В дереве на рис. 6.11 родитель узла Е — это узел В, а предки узла Е — это узлы А и В, для которых узел Е — потомок. Потомками узла А (корня дерева) являются все остальные узлы.
Высота дерева — это наибольшее расстояние (количество дуг) от корня до листа.
Высота дерева, приведённого на рис. 6.11, равна 2.
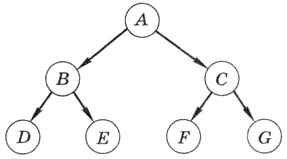
Рис. 6.11
Формально дерево можно определить следующим образом:
1) пустая структура — это дерево;
2) дерево — это корень и несколько связанных с ним отдельных (не связанных между собой) деревьев.
Здесь множество объектов (деревьев) определяется через само это множество на основе простого базового случая (пустого дерева). Такой приём называется рекурсией (см. главу 8 учебника для 10 класса). Согласно этому определению, дерево — это рекурсивная структура данных. Поэтому можно ожидать, что при работе с деревьями будут полезны рекурсивные алгоритмы.
Чаще всего в информатике используются двоичные (или бинарные) деревья, т. е. такие, в которых каждый узел имеет не более двух сыновей. Их также можно определить рекурсивно.
Двоичное дерево:
1) пустая структура — это двоичное дерево;
2) двоичное дерево — это корень и два связанных с ним отдельных двоичных дерева (левое и правое поддеревья).
Деревья широко применяются в следующих задачах:
• поиск в большом массиве неменяющихся данных;
• сортировка данных;
• вычисление арифметических выражений;
• оптимальное кодирование данных (метод сжатия Хаффмана).
Следующая страница 
Деревья поиска
Cкачать материалы урока
