Уроки 45 - 46
Деревья. Основные понятия
(§43. Деревья)

Содержание урока

Что такое дерево?

Деревья поиска

Обход двоичного дерева

Вычисление арифметических выражений

Использование связанных структур

Хранение двоичного дерева в массиве

Вопросы и задания

Задачи

Деревья поиска

Известно, что для того, чтобы найти заданный элемент в неупорядоченном массиве из N элементов, может понадобиться N сравнений. Теперь предположим, что элементы массива организованы в виде специальным образом построенного дерева, например как показано на рис. 6.12.

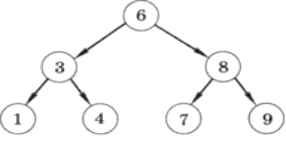
Рис. 6.12

Значения, связанные с узлами дерева, по которым выполняется поиск, называются ключами этих узлов (кроме ключа узел может содержать множество других данных). Перечислим важные свойства дерева, показанного на рис. 6.12:

• слева от каждого узла находятся узлы, ключи которых меньше или равны ключу данного узла;
• справа от каждого узла находятся узлы, ключи которых больше или равны ключу данного узла.

Дерево, обладающее такими свойствами, называется двоичным деревом поиска.

Например, пусть нужно найти узел, ключ которого равен 4. Начинаем поиск по дереву с корня. Ключ корня — 6 (больше заданного), поэтому дальше нужно искать только в левом поддереве и т. д. Если при линейном поиске в массиве за одно сравнение отсекается 1 элемент, здесь — сразу примерно половина оставшихся. Количество операций сравнения в этом случае пропорционально log₂N, т. е. алгоритм имеет асимптотическую сложность O(log₂N). Конечно, нужно учитывать, что предварительно дерево должно быть построено. Поэтому такой алгоритм выгодно применять в тех случаях, когда данные меняются редко, а поиск выполняется часто (например, в базах данных).

Следующая страница Обход двоичного дерева

Cкачать материалы урока