Урок 50
Динамическое программирование
(§45. Динамическое программирование)

Содержание урока

Что такое динамическое программирование?

Поиск оптимального решения

Количество решений

Вопросы и задания

Задачи

Поиск оптимального решения

Задача 2. В цистерне N литров молока. Есть бидоны объёмом 1, 5 и 6 литров. Нужно разлить молоко в бидоны так, чтобы все бидоны были заполнены и количество используемых бидонов было минимальным.

Человек, скорее всего, будет решать задачу перебором вариантов. Наша задача осложняется тем, что требуется написать программу, которая решает задачу для любого введённого числа N.

Самый простой подход — заполнять сначала бидоны самого большого размера (6 л), затем — меньшие и т. д. Это так называемый «жадный» алгоритм. Как вы знаете, он не всегда приводит к оптимальному решению. Например, для N — 10 «жадный» алгоритм даёт решение 6+1+1+1+1 — всего 5 бидонов, в то время как можно обойтись двумя (5 + 5).

Как и в любом решении, использующем динамическое программирование, главная задача — составить рекуррентную формулу. Сначала определим оптимальное число бидонов K_N, а потом подумаем, как определить, какие именно бидоны нужно использовать.

Представим себе, что мы выбираем бидоны постепенно. Тогда последний выбранный бидон может иметь, например, объём 1 л, в этом случае K_N = 1 + K_N-1 Если последний бидон имеет объём 5 л, то K_N = 1 + K_N-5, а если 6 л, то K_N = 1 + K_N-6. Так как нам нужно выбрать минимальное значение, то

K_N = 1 + min(K_N-1, К_N-5, K_N-6).

Вариант, выбранный при поиске минимума, определяет последний добавленный бидон, его объём нужно сохранить в отдельном массиве Р. Этот массив будет использован для определения количества выбранных бидонов каждого типа. В качестве начального значения берём К₀ = 0.

Полученная формула применима при N ≥ 6. Для меньших N используются только те данные, которые есть в таблице (рис. 6.39). Например:

К₃ = 1 + К₂ = 3, К₅ = 1 + min(K₄, К₀) = 1.

На рисунке 6.39 показаны массивы для N = 10.

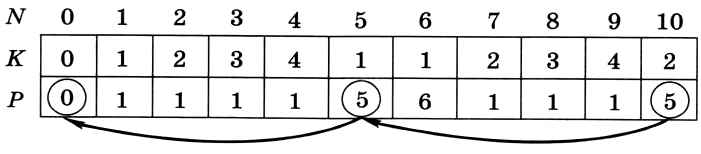
Рис. 6.39

Как по массиву Р определить оптимальный состав бидонов? Пусть, например, N = 10. Из массива Р находим, что последний добавленный бидон имеет объём 5 л. Остаётся 10 - 5 = 5 л, в элементе Р[5] тоже записано значение 5, поэтому второй бидон тоже имеет объём 5 л. Остаток 0 л означает, что мы полностью определили набор бидонов.

Можно заметить, что такая процедура очень похожа на алгоритм Дейкстры, и это не случайно. В алгоритмах Дейкстры и Флойда-Уоршелла, по сути, используется метод динамического программирования.

Задача 3 (задача о куче). Из камней весом p_i (i = 1, ..., N) требуется набрать кучу весом ровно W или, если это невозможно, максимально близкую к W (но меньшую, чем W).

Эта задача относится к трудным задачам целочисленной оптимизации, которые решаются только полным перебором вариантов. Каждый камень может входить в кучу (обозначим это состояние как 1) или не входить (0). Поэтому нужно выбрать цепочку, состоящую из N битов. При этом количество вариантов равно 2^N, и при больших N полный перебор практически невыполним.

Динамическое программирование позволяет найти решение задачи значительно быстрее. Идея состоит в том, чтобы сохранять в массиве решения всех более простых задач этого типа (при меньшем количестве камней и меньшем весе W).

Построим матрицу Т, где элемент T[i,w] — это оптимальный вес, полученный при попытке собрать кучу весом ш из г первых по счёту камней (w изменяется от 0 до W). Очевидно, что первый столбец заполнен нулями (при заданном нулевом весе никаких камней не берём).

Рассмотрим первую строку (есть только один камень). В начале этой строки будут стоять нули, а дальше, начиная со столбца р₁, — значения р₁ (взяли единственный камень). Это простые варианты задачи, решения для которых легко подсчитать вручную. Рассмотрим пример, когда требуется набрать вес 8 из камней весом 2, 4, 5 и 7 единиц (рис. 6.40).

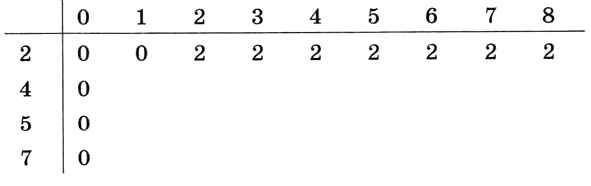
Рис. 6.40

Теперь предположим, что строки с 1-й по (i-1)-ro уже заполнены. Перейдем к i-й строке, т. е. добавим в набор i-й камень. Он может быть взят или не взят в кучу. Если мы не добавляем его в кучу, то T[i,w] = T[i-1,w], т. е. решение не меняется от добавления в набор нового камня. Если камень с весом добавлен в кучу, то остаётся «добрать» остаток оптимальным образом (используя только предыдущие камни), т. е. T[i,w] = T[i-1,w-p_i] + p_i.

Как же решить, брать или не брать камень? Надо проверить, в каком случае полученный вес будет больше (ближе к w).

Таким образом, получается рекуррентная формула для заполнения таблицы:

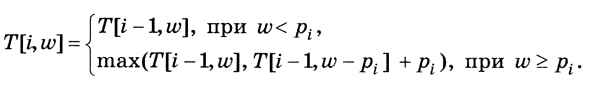
Используя эту формулу, заполняем таблицу по строкам, сверху вниз; в каждой строке — слева направо (рис. 6.41).

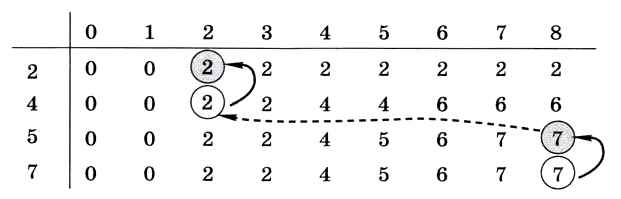
Рис. 6.41

Видим, что сумму 8 набрать невозможно, ближайшее значение — 7 (правый нижний угол таблицы).

Эта таблица содержит все необходимые данные для определения выбранной группы камней. Действительно, если камень с весом pt не включён в набор, то T[i,w] = T[i-1,w], т. е. число в таблице не меняется при переходе на строку вверх. Начинаем с правого нижнего угла таблицы, идём вверх, пока значения в столбце равны 7. Последнее такое значение — для камня с весом 5, поэтому он и выбран. Вычитая его вес из суммы, получаем 7-5 = 2, переходим во второй столбец на одну строку вверх, и снова идём вверх по столбцу, пока значение не меняется (равно 2). Так как мы успешно дошли до самого верха таблицы, взят первый камень с весом 2.

Заметим, что в рассмотренном случае есть и ещё одно решение — взять один камень с весом 7 (подумайте, как в подобных случаях находить все решения задачи).

Как мы уже отмечали, количество вариантов в задаче для N камней равно 2^N, т. е. алгоритм полного перебора имеет асимптотическую сложность 0(2^N). В данном алгоритме количество операций равно числу элементов таблицы, т. е. сложность нашего алгоритма — 0(N • w). Однако нельзя сказать, что он имеет линейную сложность, так как есть ещё сильная зависимость от заданного веса w. Такие алгоритмы называют псевдополиноми- альными. В них ускорение вычислений достигается за счёт использования дополнительной памяти для хранения промежуточных результатов.

Следующая страница Количество решений

Cкачать материалы урока