Урок 50
Динамическое программирование
(§45. Динамическое программирование)

Содержание урока

Что такое динамическое программирование?

Поиск оптимального решения

Количество решений

Вопросы и задания

Задачи

Количество решений

Задача 4. У исполнителя Утроитель две команды, которым присвоены номера:

1) прибавь 1

2) умножь на 3

Первая из них увеличивает число на экране на 1, вторая — утраивает его. Программа для Утроителя — это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число N = 20?

Заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться). Начнем с простых случаев, с которых будем начинать вычисления. Понятно, что для N = 1 существует только одна программа — пустая, не содержащая ни одной команды. Для N = 2 есть тоже только одна программа, состоящая из команды сложения. Если через K_N обозначить количество разных программ для получения числа N из 1, то К₁ = К₂ = 1.

Теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую KN с предыдущими элементами последовательности К₁, К₂, ..., K_N, т. е. с решениями таких же задач для меньших N.

Если число N не делится на 3, то последней командой для его получения может быть только операция сложения, поэтому K_N = K_N-1. Если N делится на 3, то последней командой может быть как сложение, так и умножение. Поэтому нужно сложить K_N-1 (количество программ с последней командой сложения) и K_N/3 (количество программ с последней командой умножения). В итоге получаем:

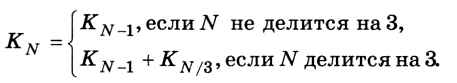
Остаётся заполнить таблицу для всех значений от 1 до заданного N = 20. Для небольших значений эту задачу легко решить вручную:

Заметим, что количество вариантов меняется только в тех столбцах, где N делится на 3, поэтому из всей таблицы можно оставить только эти столбцы (и добавив следующее значение, кратное трём):

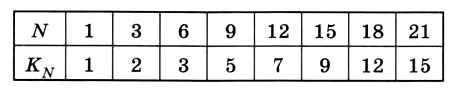
Заданное число 20 попадает в последний интервал (от 18 до 21), поэтому ответ в данной задаче — 12.

При составлении программы с полной таблицей нужно выделить в памяти целочисленный массив К, индексы которого изменяются от 1 до N, и заполнить его по приведённым выше формулам:

К[1]:=1;
for i:=2 to N do begin
	K[i]:=K[i—1];
	if i mod 3=0 then
		К[i]:=K[i]+K[i div 3];
end;

Ответом будет значение K[N].

Задача 5 (размен монет). Сколькими различными способами можно выдать сдачу размером W рублей, если есть монеты достоинством p_i (i = 1, ..., N)? Для того чтобы сдачу всегда можно было выдать, будем предполагать, что в наборе есть монета достоинством 1 рубль (p₁ = 1).

Это задача, так же, как и задача о куче, решается только полным перебором вариантов, число которых при больших N очень велико. Будем использовать динамическое программирование, сохраняя в массиве решения всех задач меньшей размерности (для меньших значений N и W).

В матрице Т значение T[i,w] будет обозначать количество вариантов сдачи размером w рублей (w изменяется от 0 до W) при использовании первых i монет из набора. Очевидно, что при нулевой сдаче есть только один вариант (не дать ни одной монеты), так же и при наличии только одного типа монет (напомним, что p₁ = 1) есть тоже только один вариант. Поэтому нулевой столбец и первую строку таблицы можно заполнить сразу единицами. Для примера мы будем рассматривать задачу для W = 10 и набора монет достоинством 1, 2, 5 и 10 рублей (рис. 6.42).

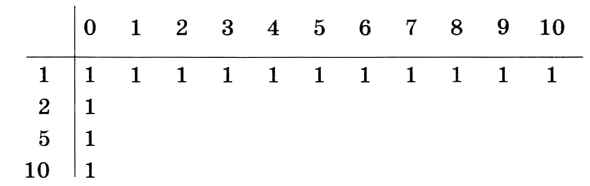
Рис. 6.42

Таким образом, мы определили простые базовые случаи, от которых «отталкивается» рекуррентная формула.

Теперь рассмотрим общий случай. Заполнять таблицу будем по строкам, слева направо. Для вычисления T[i,w] предположим, что мы добавляем в набор монету достоинством р_i. Если сумма w меньше, чем р_i, то количество вариантов не увеличивается, и T[i,w] = T[i- 1,w]. Если сумма больше р_i то к этому значению нужно добавить количество вариантов с «участием» новой монеты. Если монета достоинством p_i использована, то нужно учесть все варианты «разложения» остатка w-p_i на все доступные монеты, т. е. T[i,w] = T[i-1,w] + T[i,w -p_i]. В итоге получается рекуррентная формула

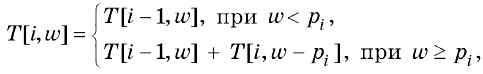
которая используется для заполнения таблицы (рис. 6.43).

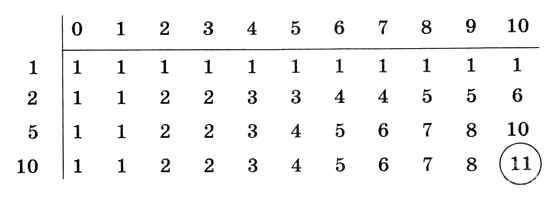
Рис. 6.43

Ответ к задаче находится в правом нижнем углу таблицы.

Вы могли заметить, что решение этой задачи очень похоже на решение задачи о куче камней. Это не случайно, две эти задачи относятся к классу сложных задач, для решения которых известны только переборные алгоритмы. Использование методов динамического программирования позволяет ускорить решение за счёт хранения промежуточных результатов, однако требует дополнительного расхода памяти.

Следующая страница Вопросы и задания

Cкачать материалы урока