Урок 5
§4. Инструменты анализа данных

4.1. Диаграммы

Как правило, электронные таблицы содержат большое количество числовых данных, которые требуется сравнивать, оценивать их изменение с течением времени, определять соотношение между ними т. д. Проводить подобный анализ большого количества числовых данных значительно легче, если изобразить их графически (визуализировать). Для графического представления числовых данных используются диаграммы.

Диаграмма — это графическое представление числовых данных, позволяющее быстро оценить соотношение нескольких величин.

Табличные процессоры позволяют строить диаграммы следующих типов:

• гистограмма;
• диаграмма с областями;
• линейчатая диаграмма;
• поверхностная диаграмма;
• круговая диаграмма;
• график;
• лепестковая диаграмма и др.

Чтобы в Microsoft Excel просмотреть все доступные типы диаграмм, изучите группу Диаграммы на вкладке Вставка (рис. 1.8).

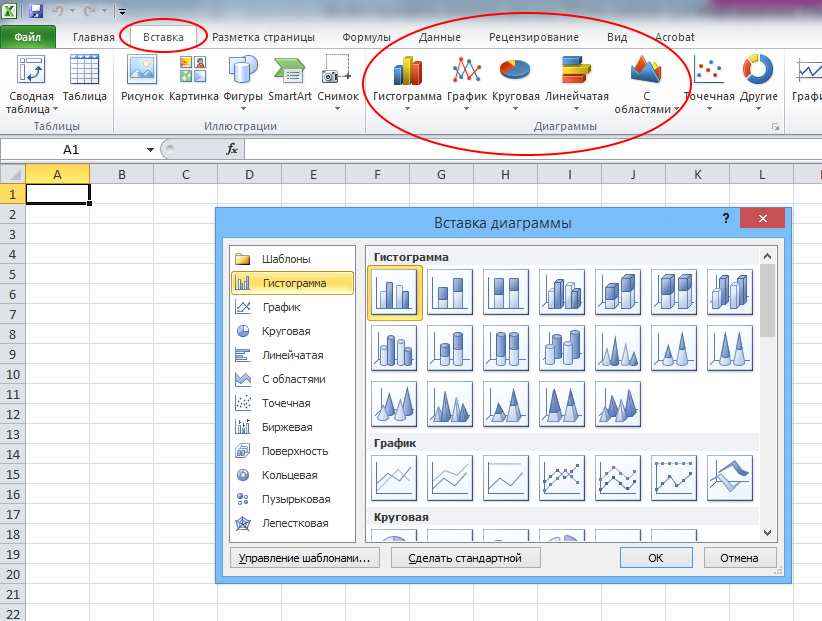
Рис. 1.8. Типы диаграмм в Microsoft Excel

Выясните, какие типы диаграмм можно создавать в табличном процессоре, имеющемся в вашем распоряжении.

В диаграмме любого типа можно выделить следующие объекты (рис. 1.9):

1 — область диаграммы (в ней размещаются все объекты диаграммы);
2 — название диаграммы, чётко описывающее то, что представлено на диаграмме;
3 — область построения диаграммы (непосредственно в ней располагается сама диаграмма);
4 — ось значений (вертикальная, ось Y). На ней находится шкала с определённым шагом, устанавливаемым автоматически, в зависимости от наименьшего и наибольшего значений данных, изображённых на диаграмме. Именно по этой шкале можно оценить данные, представленные на диаграмме;
5 — ряды данных — наборы числовых данных, некоторым образом связанных между собой и размещённых в электронной таблице в одной строке или столбце. На диаграмме ряд данных изображается геометрическими фигурами одного вида и цвета;
6 — ось категорий (горизонтальная, ось X). На ней отображаются значения определённого свойства данных;
7 — легенда, поясняющая соответствие между названиями рядов и используемыми на диаграмме цветами. По умолчанию названия рядов являются названиями строк (или столбцов) диапазона данных, по которым построена диаграмма;
8 — названия осей.

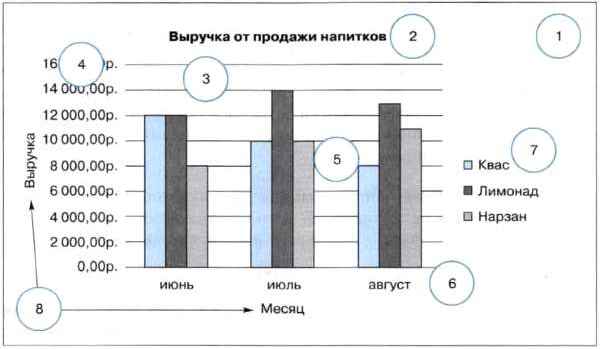
Рис. 1.9. Основные элементы диаграммы

Воспроизведите в табличном процессоре диаграмму, представленную на рисунке 1.9. С помощью контекстного меню исследуйте свойства каждого объекта этой диаграммы.

На диаграммах разных типов числовые данные могут быть представлены точками, отрезками, прямоугольниками, секторами круга, прямоугольными параллелепипедами, цилиндрами, конусами и другими геометрическими фигурами. При этом размеры геометрических фигур или расстояния от них до осей пропорциональны числовым данным, которые они отображают.

Диаграммы, создаваемые в электронных таблицах, динамические — при редактировании данных в таблице размеры или количество фигур, обозначающих эти данные, автоматически изменяются.

Вспомните основные приёмы построения диаграмм, известные вам из курса информатики основной школы.

Рассмотрим самые распространённые типы диаграмм.

Гистограммы целесообразно создавать тогда, когда нужно сравнить значения нескольких наборов данных, графически изобразить отличия значений одних наборов данных от других, показать изменения данных с течением времени.

Различают следующие виды гистограмм:

• гистограмма с группировкой;
• гистограмма с накоплением;
• нормированная гистограмма с накоплением;
• объёмная гистограмма.

В гистограмме с группировкой прямоугольники, которые являются графическими изображениями числовых данных из разных наборов, располагаются рядом друг с другом (см. рис. 1.9). В гистограмме с накоплением прямоугольники, изображающие числовые данные, располагаются друг над другом (рис. 1.10). Это даёт возможность оценить суммарные данные и вклад каждой составляющей в общую сумму.

В нормированной гистограмме с накоплением вертикальная ось имеет шкалу в процентах. Это даёт возможность оценить долю (процентную часть) данных в общей сумме (рис. 1.11).

Подумайте, по какой из трёх диаграмм проще всего определить:

1) продажа каких напитков неуклонно возрастала;
2) продажа каких напитков принесла наибольшую прибыль в июле;
3) динамику изменений суммарной выручки от продажи всех трёх напитков;
4) вклад от продажи каждого напитка в общую выручку.

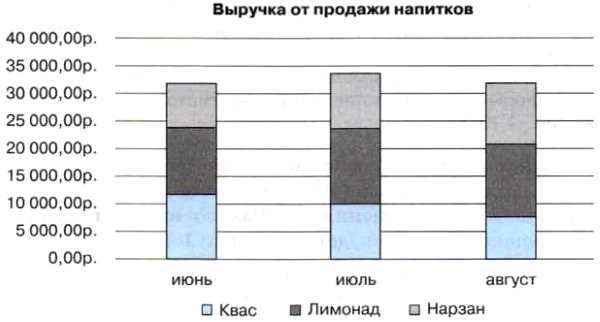
Рис. 1.10. Пример гистограммы с накоплением

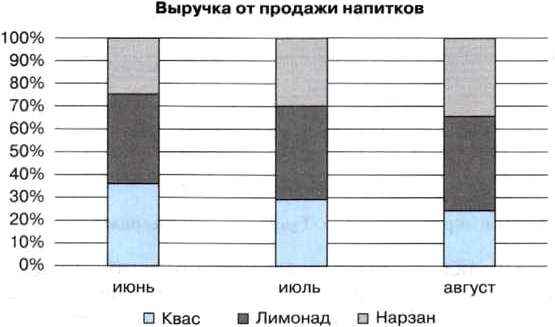
Рис. 1.11. Нормированная гистограмма с накоплением

Линейчатые диаграммы аналогичны гистограммам и отличаются от них лишь горизонтальным расположением геометрических фигур.

К типу диаграмм Круговая относятся плоские и объёмные круговые диаграммы. Их целесообразно использовать тогда, когда нужно отобразить части одного целого, сравнить соотношение частей между собой и отношение частей к целому.

Круговые диаграммы позволяют отобразить только один ряд данных. Они теряют наглядность, если содержат много элементов данных. Несколько круговых диаграмм можно заменить, например, одной нормированной гистограммой с накоплением.

Подумайте, сколько разных круговых диаграмм можно построить по информации, содержащейся в диаграмме, представленной на рисунке 1.9.

Сколько круговых диаграмм потребуется для того, чтобы изобразить информацию, представленную на гистограмме с накоплением (см. рис. 1.10)?

Диаграммы типа График целесообразно использовать, если количество данных в наборе достаточно большое, если нужно отобразить динамику изменения данных во времени, сравнить изменения нескольких рядов данных (рис. 1.12).

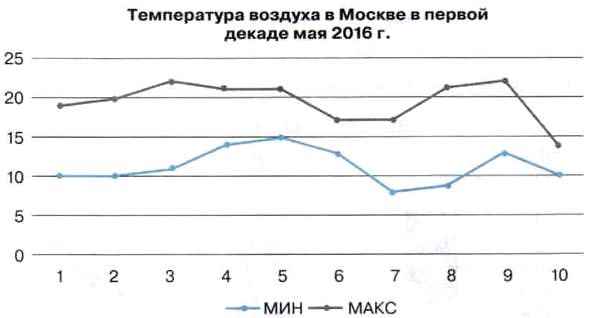
Рис. 1.12. Пример диаграммы График с маркерами

Точечные диаграммы с гладкими кривыми можно использовать для построения графиков функций, предварительно заполнив диапазон ячеек значениями аргумента и соответствующими значениями функции. Можно построить на одной диаграмме графики двух функций и использовать их для приближённого решения уравнения.

Пример. Найдём на отрезке [0; 1,2] корень уравнения 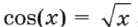, построив в табличном процессоре графики функций, соответствующих левой и правой частям равенства.

Для этого:

1) используя стандартные функции COS и КОРЕНЬ, построим таблицу значений функций для х, изменяющегося с шагом 0,1:

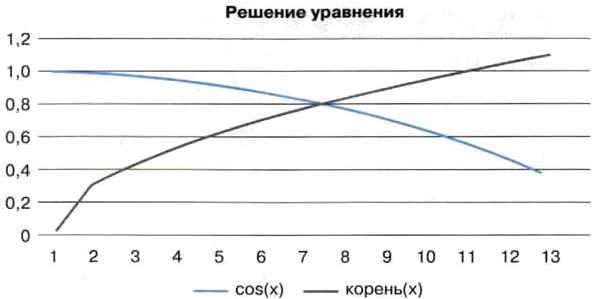
Рис. 1.13. Графики функций

2) по значениям диапазона B2:N3 построим графики функций COS(x) и КОРЕНЬ(х) (рис. 1.13);

3) заменим номера точек, проставленные по горизонтальной оси, на значения аргумента х рассматриваемых функций. Для этого вызовем контекстное меню горизонтальной оси и выберем пункт Выбрать данные. Появится окно Выбор источника данных (рис. 1.14).

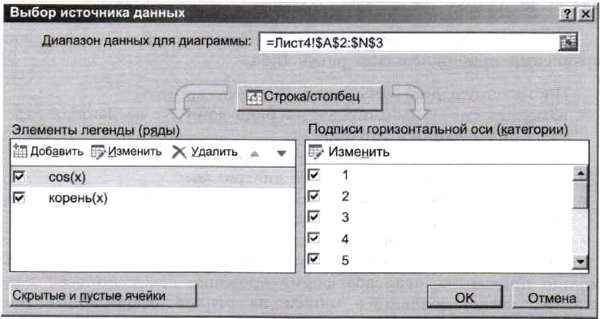
Рис. 1.14. Окно Выбор источника данных

В открывшемся окне нажмём на кнопку изменения подписей горизонтальной оси и выберем диапазон со значениями аргумента (рис. 1.15).

Рис. 1.15. Окно Подписи оси

После редактирования (совмещения) точки пересечения осей и добавления вертикальных линий сетки график приобретёт вид, представленный на рисунке 1.16.

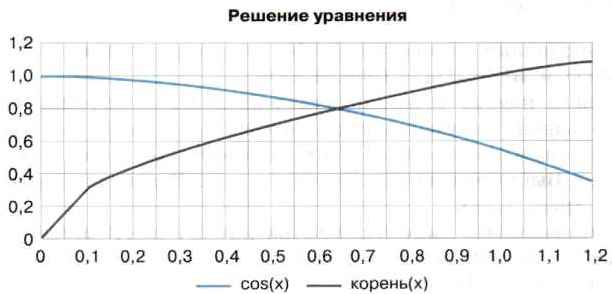
Рис. 1.16. График после редактирования

В результате построения графиков функций видно, что корень уравнения приблизительно равен 0,64.

Построенную диаграмму можно редактировать:

• изменять способ формирования ряда данных: из данных строки или из данных столбца;
• изменять диапазон ячеек, по которым строится диаграмма;
• изменять тип, вид или макет диаграммы;
• вставлять, перемещать, удалять или изменять название диаграммы, легенды, подписей данных;
• изменять отображение осей и линий сетки и др. Построенную диаграмму можно форматировать. При этом можно применить стилевое форматирование сразу ко всей диаграмме, воспользовавшись одним из стилей оформления диаграмм. Кроме того, можно форматировать отдельные объекты диаграммы, которые предварительно надо выделить.

Некоторые объекты диаграммы, например ряд, состоят из нескольких частей. Чтобы выделить только одну часть, например отдельную точку ряда, необходимо сначала выделить весь объект, а затем выбрать нужную его часть.

Cкачать материалы урока