Урок 12
§8. Структурированные типы данных. Массивы

8.5. Перестановка всёх элементов массива в обратном порядке

Пример 10. Перестановка всех элементов массива а[1..n] в обратном порядке сводится к тому, что меняются местами первый и последний элементы, второй и предпоследний элементы и т. д.

Перестановка нашего массива из семи элементов даст такой результат:

Вспомним, как можно произвести обмен значений между двумя переменными. Выполнение операторов:

а[1]:=а[n]; а[n]:=а[1]; к желаемому результату не приводит. Самый простой вариант — использование вспомогательной переменной:

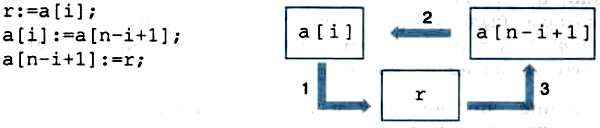
Выясним, сколько всего операций обмена следует произвести.

Если произведена перестановка, например, первого и последнего элементов, то одновременно произведена и перестановка последнего и первого элементов. Таким образом, если число элементов массива чётное, то достаточно произвести n/2 операций обмена.

Но что происходит, если массив содержит нечётное число элементов? Например, в нашем массиве из семи элементов выполнялось три обмена, а четвёртый элемент, занимающий центральную позицию, оставался на своём месте. В общем случае число операций обмена при перестановке в обратном порядке всех n элементов массива определяется как n div 2.

В общем случае, фрагмент программы по перестановке в обратном порядке всех элементов массива а[1..n] имеет вид:

Запишите полный текст программы и выполните её на компьютере для рассмотренного выше массива а, состоящего из семи и из шести элементов.

8.6. Сортировка массива

Сортировка — один из наиболее распространённых процессов современной обработки данных.

Сортировка — это распределение элементов массива в соответствии с определёнными правилами.

Под сортировкой (упорядочением) массива понимают перераспределение значений его элементов в некотором определённом порядке.

Порядок, при котором в массиве первый элемент имеет самое маленькое значение, а значение каждого следующего элемента не меньше значения предыдущего элемента, называют неубывающим.

Порядок, при котором в массиве первый элемент имеет самое большое значение, а значение каждого следующего элемента не больше значения предыдущего элемента, называют невозрастающим.

Цель сортировки — ускорить последующий поиск элементов, т. к. нужный элемент легче искать в упорядоченном массиве.

Рассмотрим и проанализируем несколько алгоритмов сортировки для решения следующей задачи. Дан одномерный массив целых чисел. Требуется отсортировать его так, чтобы все элементы были расположены в порядке неубывания: a[i] <= a[i 4- 1].

Обменная сортировка методом «пузырька»

Своё название алгоритм получил благодаря следующей ассоциации: если сортировать этим алгоритмом массив по неубыванию, то максимальный элемент «тонет», а «лёгкие» элементы поднимаются на одну позицию к началу массива на каждом шаге алгоритма.

Пусть n — количество элементов в неупорядоченном массиве.

1. Поместим на место п-го элемента (а[n]) наибольший элемент массива. Для этого:

1) положим i = l;
2) пока не обработана последняя пара элементов, т. е. (n - 1)-й и n-й элементы:
• сравниваем i-и и (i + 1)-й элементы массива;
• если a[i] > a[i +1] (элементы расположены не по порядку), то меняем элементы местами;
• переходим к следующей паре элементов, сдвинувшись на один элемент вправо.

2. Повторяем пункт 1, каждый раз уменьшая размерность неупорядоченного массива на 1, до тех пор, пока не будет обработан массив из одной пары элементов (таким образом, на k-м просмотре будут сравниваться первые (n - k) элементов со своими соседями справа).

Пример 11. Есть массив: 5 4 3 2 1. На примере этого массива подсчитаем количество элементарных действий в вычислительном процессе алгоритма сортировки методом «пузырька»:

• 1-я итерация: 4 3 2 1 5 (4 сравнения, 4 обмена);
• 2-я итерация: 3 2 1 4 5 (3 сравнения, 3 обмена);
• 3-я итерация: 2 1 3 4 5 (2 сравнения, 2 обмена);
• 4-я итерация: 1 2 3 4 5 (1 сравнение, 1 обмен).

Алгоритм закончил работу. Было сделано 10 сравнений и 10 обменов (4 + 3 + 2 + 1).

Этот алгоритм легко запоминается, но на практике он используется достаточно редко из-за квадратичной сложности, означающей, что в общем случае количество выполненных сравнений и обменов сопоставимо с п2, где тг — количество элементов массива.

Попытайтесь самостоятельно запрограммировать алгоритм сортировки методом «пузырька».

Сортировка выбором

Сортировка выбором (в порядке неубывания) осуществляется следующим образом:

1) в массиве выбирается минимальный элемент;
2) минимальный и первый элементы меняются местами (первый элемент считается отсортированным);
3) в неотсортированной части массива снова выбирается минимальный элемент и меняется местами с первым неотсортированным элементом массива;
4) действия, описанные в пункте 3, повторяются с неотсортированными элементами массива до тех пор, пока не останется один неотсортированный элемент (его значение будет максимальным).

Пример 12. Есть массив: 5 4 3 2 1.

1- я итерация: 1 4 3 2 5 (4 сравнения, 1 обмен).
2- я итерация: 1 2 3 4 5 (3 сравнения, 1 обмен).
3- я итерация: 1 2 3 4 5 (2 сравнения, 0 обменов).
4- я итерация: 1 2 3 4 5 (1 сравнение, 0 обменов).

В общем случае алгоритм сортировки выбором имеет квадратичную сложность относительно операций сравнения и линейную сложность относительно операций обменов. Этот алгоритм целесообразно применять, когда операция обмена над элементами массива особенно трудоёмка (например, если элементом массива является запись с большим числом полей).

Приведём фрагмент программы, реализующей описанный выше алгоритм:

Запишите полный текст программы и выполните её на компьютере для рассмотренного выше массива.

Cкачать материалы урока