Урок 17
§11.1. Моделирование на графах

11.1. Алгоритмы нахождения кратчайших путей между вершинами графа (Алгоритм Дейкстры)

Алгоритм Дейкстры служит для нахождения кратчайшего пути между одной конкретной вершиной (источником) и всеми остальными вершинами графа.

Суть алгоритма состоит в следующем. Каждой вершине графа ставится в соответствие метка — минимальное известное расстояние от источника до этой вершины. Метка самого источника полагается равной 0. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки.

На первом шаге расстояние от источника до всех остальных вершин неизвестно. Метки вершин (кроме источника) считаются равными бесконечности, все вершины считаются непосещёнными.

Далее, из всех непосещённых вершин выбирается вершина, имеющая минимальную метку. Для каждого из соседей этой вершины (кроме отмеченных как посещённые) рассчитывается новая длина пути, как сумма значений текущей метки этой вершины и длины ребра, соединяющего её с соседом. Если полученное значение длины меньше значения метки соседа, то значение метки заменяется полученным значением длины. После рассмотрения всех соседей вершина помечается как посещённая. Этот шаг алгоритма повторяется, пока есть непосещённые вершины. Работа алгоритма завершается, когда все вершины посещены.

Рассмотрим работу алгоритма на примере. На рисунке 3.12 кружками обозначены вершины графа, в кружки вписаны имена вершин. Вершины соединены линиями — рёбрами графа. Около каждого ребра обозначен его «вес» — длина пути. Рядом с каждой вершиной дана метка — длина кратчайшего пути в эту вершину из вершины А: для вершины А — это 0, для всех других вершин она неизвестна и обозначена знаком «бесконечность».

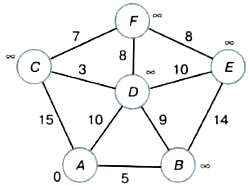
Рис. 3.12. Алгоритм Дейкстры. Начальное состояние

Минимальную метку (0) имеет вершина А. Её соседи — вершины В, С, D. Очерёдность рассмотрения соседей: В, D, С. После изменения их меток получим результат, представленный на рисунке 3.13.

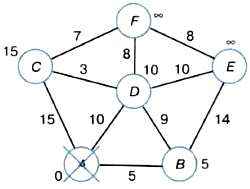
Рис. 3.13. Алгоритм Дейкстры. Шаг 1

После изменения меток всех соседей вершины А она помечается как просмотренная. Теперь минимальная метка из непросмотренных вершин у вершины В. Её соседи — вершины D и Е. Так как 5 + 9 > 10, метка вершины D не изменяется. Вершина Е получает метку 19 (рис. 3.14).

Теперь минимальная метка из непросмотренных вершин у вершины D. Её соседи — вершины С, Е и F. Так как 10 + 3 < 15, метка вершины С изменяется. Вершина F получает метку 18. Метка вершины Е не изменяется (рис. 3.15).

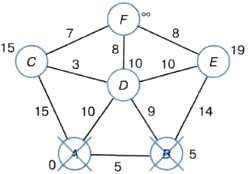
Рис. 3.14. Алгоритм Дейкстры. Шаг 2

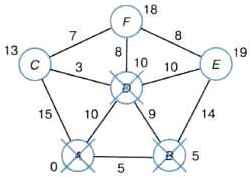
Рис. 3.15. Алгоритм Дейкстры. Шаг 3

Далее в качестве вершин с минимальными метками будут поочерёдно рассматриваться вершины С, F и Е. К изменению меток соседних с ними вершин это не приведёт (рис. 3.16).

Полученные в результате работы алгоритма метки вершин графа — это и есть кратчайшие расстояния от вершины А до каждой из этих вершин.

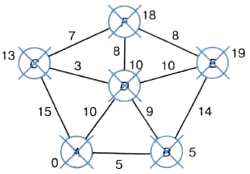
Рис. 3.16. Алгоритм Дейкстры. Результат работы

Cкачать материалы урока