Уроки 8 - 10
§1.3. Приближенное решение уравнений

Содержание урока

1.3.1. Графические и численные методы решения уравнений

1.3.2. Приближенное решение уравнений на языке Visual Basic

1.3.3. Приближенное решение уравнений на языке Turbo Delphi

1.3.4. Приближенное решение уравнений в электронных таблицах

Задача

Проект «Приближенное решение уравнения» в электронных таблицах

Контрольные вопросы

1.3.4. Приближенное решение уравнений в электронных таблицах

Проект «Приближенное решение уравнения» в электронных таблицах

1. Представить заданное уравнение в табличной форме (рис. 1.16).

Рис. 1.16. Табличное представление уравнения

2. Для грубо приближенного определения корня построить диаграмму типа График.

По графику грубо приближенно можно определить, что x ≈ 0,8 (рис. 1.17).

Рис. 1.17. График функции

Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой).

Методом подбора параметра необходимо определить значение аргумента х (ячейка F1), при котором значение функции y (ячейка F2) будет равно нулю.

3. Выделить ячейку со значением функции F2 и ввести команду [Сервис-Подбор параметра...] в Microsoft Excel 2003 и OpenOffice.org Calc или команду [Анализ "что-если"- Подбор параметра...] в Microsoft Excel 2007.

4. В диалоговом окне Подбор параметра (рис. 1.18):

• в поле Установить в ячейке: ввести адрес ячейки $F$2;
• в поле Значение: ввести требуемое значение функции (в данном случае 0);
• в поле Изменяя значение ячейки: ввести адрес ячейки $F$1, в которой будет производиться подбор значения аргумента.

Щелкнуть по кнопке ОК.

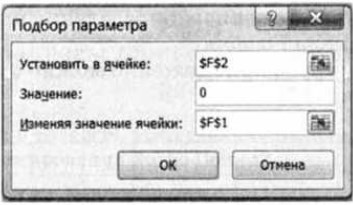
Рис. 1.18. Диалоговое окно надстройки Подбор параметра

5. На панели Результат подбора параметра будет выведена информация о величине значения в ячейке F2 (рис. 1.19).

Рис. 1.19. Информационная панель надстройки Подбор параметра

6. В ячейке аргумента F1 появится подобранное значение 0,855. Таким образом, корень уравнения x ≈ 0,855 найден с заданной точностью.

Следующая страница Контрольные вопросы

Cкачать материалы урока