Уроки 11 - 12
§1.4. Вероятностные модели

Содержание урока

1.4.1. Построение информационной модели с использованием метода Монте-Карло

Описательная модель вычисления площадей геометрических фигур с использованием метода Монте-Карло

Формальная модель «Определение площади круга методом Монте-Карло»

Контрольные вопросы

1.4.2. Компьютерные модели, построенные с использованием метода Монте-Карло, на языке Visual Basic

1.4.3. Компьютерные модели, построенные с использованием метода Монте-Карло, на языке Turbo Delphi

1.4.1. Построение информационной модели с использованием метода Монте-Карло

Формальная модель «Определение площади круга методом Монте-Карло»

Построим формальную модель для вычисления площади круга радиуса r, центр которого совпадает с началом координат.

Круг вписан в квадрат со стороной 2 • r, тогда площадь квадрата можно вычислить по формуле:

S₁ = 4 • r².

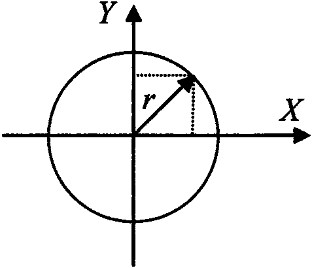
Рис. 1.20. Круг, вписанный в квадрат

Пусть N — количество точек, которые случайным образом генерируются внутри квадрата. Случайный выбор координат точек, которые попадают внутрь квадрата (N точек), должен производиться так, чтобы координаты точек x и y удовлетворяли условиям:

-r ≤ x ≤ r и -r ≤ y ≤ r.

Пусть М — количество точек, попавших внутрь круга, их координаты удовлетворяют условию:

x² + у² ≤ r².

Предположим, что отношение площадей круга S₂ квадрата S₁ равно отношению количества точек М, попавших внутрь круга, к количеству точек N, попавших внут квадрата, тогда получим формулу:

S₂/S₁ = M/N.

Тогда площадь круга можно вычислить в единицах измерения радиуса по формуле:

S₂ = S₁ • M/N = 4r² • M/N.

Более того, таким способом можно вычислить значение числа π. Подставим в формулу значение площади круга S₂ = πr² и получим формулу для вычисления числа π:

π • r² = 4r² • M/N;

π = 4 • M/N.

Следующая страница Контрольные вопросы

Cкачать материалы урока