Уроки 22 - 26
§1.8. Модели логических устройств
Содержание урока
1.8.1. Логические схемы полусумматора и триггера
Полусумматор
1.8.2. Модели логических устройств компьютера на языке Visual Basic
1.8.3. Модели логических устройств компьютера на языке Turbo Delphi
1.8.4. Модели логических устройств компьютера в электронных таблицах
1.8.1. Логические схемы полусумматора и триггера
Полусумматор
При изучении базовых логических устройств компьютера (сумматор, триггер) целесообразно использовать компьютерные модели. Такие модели позволяют визуализировать процесс преобразования логических значений входных сигналов в значения выходных сигналов.
Полусумматор. Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в старший разряд. Обозначим слагаемые А, В, перенос Р и сумму S. Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом (табл. 1.3).
Таблица 1.3. Таблица сложения с учетом переноса
| Слагаемые | Перенос | Сумма | |
| A | B | P | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:
Р = А & В.
Получим теперь формулу для вычисления суммы. Значения суммы более всего совпадают с результатом операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
S = (A ∨ В) & (А & В).
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предположения (табл. 1.4).
Таблица 1.4. Таблица истинности логической функции S = (A ∨ В) & (А & В)
| A | B | A ∨ В | А & В | (А & В) | (A ∨ В) & (А & В) |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему полусумматора. Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел А и В без учета переноса из младшего разряда.
По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент И.
Анализ логической формулы для суммы показывает, что на выходе должен стоять элемент логического умножения И, который имеет два входа. На один из входов подается результат логического сложения исходных величин A ∨ В, т. е. на него должен подаваться сигнал с элемента логического сложения ИЛИ.
На второй вход требуется подать результат инвертированного логического умножения исходных сигналов А & В, т. е. на второй вход подается сигнал с элемента НЕ, на вход которого, в свою очередь, поступает сигнал с элемента логического умножения И (рис. 1.39).
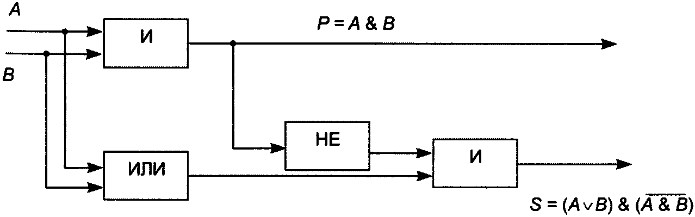
Рис. 1.39. Логическая схема полусумматора
Следующая страница  Триггер
Триггер

