Уроки 35 - 36
Самостоятельная работа. Контрольная работа
Содержание урока
Самостоятельная работа
Проект "Бросание мячика в стенку" на языке Visual Basic
Проект "Диапазон углов" на языке Visual Basic
Проект "Бросание мячика в стенку" на языке Lazarus / Delphi
Контрольная работа
Самостоятельная работа
Проект "Бросание мячика в стенку" на языке Lazarus / Delphi
Для выполнения практической работы вам потребуется язык программирования Turbo Delphi, но в силу того, что Delphi сейчас нигде не распространяется на бесплатной основе, нам нужна будет альтернатива. И она есть, программа Lazarus, которая при том является кроссплатформенной. Это значит, что она есть и на Windows, и на Linux и даже на Mac.
Программу Lazarus для Windows (32/64) можно скачать по этой ссылке.
Компьютерная модель движения тела на языке Lazarus / Delphi
На основе формальной модели, описывающей движение тела, брошенного под углом к горизонту, создадим компьютерную модель с использованием системы программирования Lazarus / Delphi.
Проект "Бросание мячика в стенку" на языке Lazarus / TurboDelphi
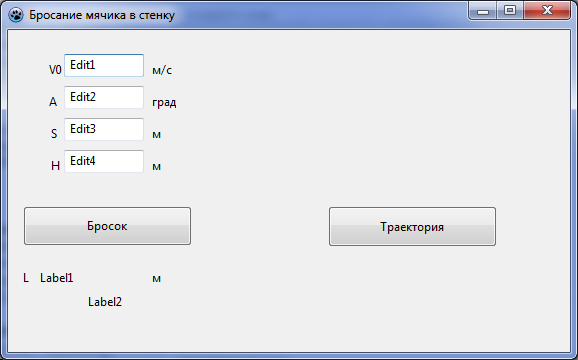
Создадим сначала графический интерфейс проекта "Бросание мячика в стенку"
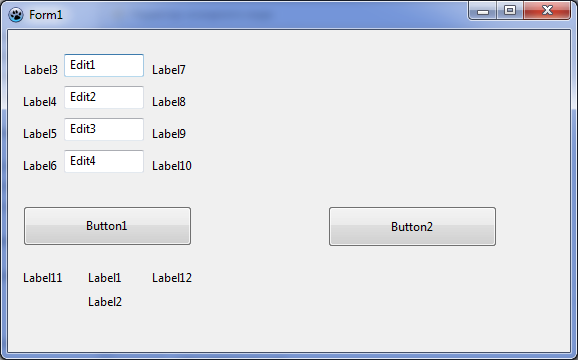
1. Разместить на форме:
- четыре текстовых поля для ввода значений:
EditV0 - начальной скорости
EditA - угла бросания мячика
EditS - расстояние до стенки
EditL - высота стенки
- надпись Label1 для вывода высоты мячика на заданном расстоянии;
- надпись Label2 для вывода текстового сообщения о результатах броска;
- десять надписей для вывода имён переменных и единиц измерения;
- кнопку Button1 для запуска событийной процедуры вычисления результатов бросания мячика;
- кнопку Button2 для демонстрации траектории движения мячика.
2. Ввести в программный код в оператор uses модуль Math, который обеспечивает подключение математических функций (Cos(), Tan() и т.д.).
Код
Windows, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, Math;
3. Объявить переменные (вещественные одинарной точности) и константы для всего проекта:
Код
V0:real;
A:real;
S:real;
H:real;
L:real;
const
G = 9.81;
Pi = 3.14;
4. Создать программный код событийной процедуры TForm1.Button1Click, определяющей попадание мячика в стенку. В этом коде:
- объявить вещественную переменную одинарной точности L для данной событийной процедуры (высота мячика l в момент попадания в стенку);
- присвоить переменным V0, A, S, H значения, введенные в текстовые поля, с использованием функции преобразования строки в вещественное число StrToFloat();
- вычислить высоту мячика L на заданном расстоянии по формуле;
- вывести высоту мячика L в поле надписи Label1;
- вывести текстовое сообщение о результатах броска в поле надписи Label2 с использованием оператора If-Then-Else, в котором в качестве условия проверяется значение переменной L.
Код
begin
V0:=StrToFloat(EditV0.Text);
A:=StrToFloat(EditA.Text) ;
S:=StrToFloat(EditS.Text);
H:=StrToFloat(EditL.Text) ;
L:=S*Tan(A*Pi/180)-G*Sqr(S)/(2*Sqr(V0*Cos(A*Pi/180)));
Label1.Caption:=FloatToStr(L);
if L<0 then Label2.Caption:='Недолёт'
else if L > H then Label2.Caption:='Перелёт'
else Label2.Caption:='Попадание';
end;
Для визуализации формальной модели построим траекторию движения тела (график зависимости высоты мячика над поверхностью земли от дальности полёта). Снабдим график осями координат со шкалами и выведем положительные стенки.
5. Поместить на форму графическое поле Image1, в котором будет осуществляться построение графика. С помощью диалогового окна Инспектор объектов установить размеры графического поля, например свойству Height присвоить значение 200, а Width - 400.
6. Создать событийную процедуру TForm1.Button2Click, в которой:
- объявить вещественную переменную T (время);
- объявить целочисленные переменные X, Y и N (координаты мячика и счетчик цикла);
- присвоить переменные V0, A, S, H значения, введенные в текстовые поля, с использования функции преобразования строки в вещественное число StrToFloat();
- построить траекторию движения мячика на объекте Image1.Canvas;
- построить оси X и Y со шкалами и стенку.
Функция Round() необходима, чтобы преобразовывать вещественные переменные одинарной точности в целочисленные переменные (значения координат).
Код
var
X:integer;
Y:integer;
T:real;
N:integer;
begin
V0:=StrToFloat(EditV0.Text);
A:=StrToFloat(EditA.Text);
S:=StrToFloat(EditS.Text);
H:=StrToFloat(EditL.Text);
Image1.Canvas.Clear;
Image1.Canvas.Clear;
with Image1.Canvas do
while T<5 Do
begin
T:=T+0.005;
Y:=180-Round(10*(V0*Sin(A*Pi/180)*T-G*T*T/2));
X:=5+Round(10*(V0*Cos(A*Pi/180)*T));
Pixels[X,Y]:=clWhite;
MoveTo(0,180);LineTo(400,180);
MoveTo(5,0);LineTo(5,400);
MoveTo(Round(5+10*S), Round(180));
LineTo(Round(5+10*S), 180-Round(10*H));
N:=0;
while N<400 do
begin
N:=N+50;
MoveTo(5+N, 180); LineTo(5+N,200);
TextOut(7+N,180,IntToStr(Round(N/10)));
end;
N:=0;
while N<200 do
begin
N:=N+50;
MoveTo(0,180-N);LineTo(10,180-N);
TextOut(0,180-N, IntToStr(Round(N/10)));
end;
end;
end;
7. Запустить проект и ввести значения начальной скорости, угла бросания, расстояния до стенки и её высоты. Щёлкнуть по кнопке Бросок. В поля меток будут выведены значения координаты мячика и результаты броска. Щёлкнуть по кнопке Траектория. В графическом поле появится траектория движения тела. Подобрать значения начальной скорости и угла бросания мячика, обеспечивающие его попадание в стенку.
Например, при скорости бросания мячика V0 = 18 м/с и угле бросания α = 34° мячик попадает в стенку высотой h=1 м, находящуюся на расстоянии S=30 м на высоте l=0,406314279729352 м.
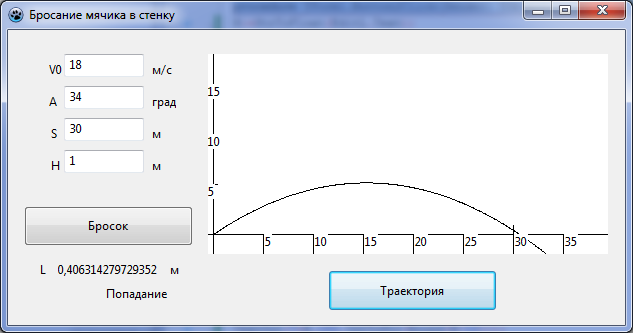
Анализ результатов. Полученная точность высоты попадания мячика в стенку l=0, 406314279729352 м не имеет физического смысла и определяется типом переменной. Значение переменной типа Real вычисляется с точностью 15 значащих цифр, однако исходные данные заданы с точностью две значащие цифры, поэтому целесообразно результат округлить до трёх значащих цифр: l = 0,406 м.
Корректировка модели. Модернизируем проект так, чтобы для каждого значения скорости бросания получить диапазон значений углов, обеспечивающих попадание мячика в стенку.
Для этого необходимо в цикле со счетчиком по углу бросания вычислить положение мячика на расстоянии стенки и определить те углы, которые соответствуют высоте стенки.
Источник: http://informat45.ucoz.ru/forum/3-290-1
Следующая страница  Контрольная работа
Контрольная работа

