Урок 22
Информационные модели на графах
Использование графов при решении задач
Практическая работа №14
«Создаём информационные модели – схемы, графы, деревья» (задания 4 и 6)
Содержание урока
Информационные модели на графах
Использование графов при решении задач
Компьютерный практикум. Ресурсы ЕК ЦОР. Задания 1 - 7
Информационные модели на графах
• схема
• граф
• сеть
• дерево
Наглядным средством представления состава и структуры системы является граф. Граф состоит из вершин, связанных линиями. Если линия направленная (со стрелкой), то она называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей. Вершины могут изображаться кругами, овалами, точками, прямоугольниками и т. д.
Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель рассматриваемой системы в форме графа.
Ранее мы рассматривали графы — схемы отношений, отражающие имеющиеся связи между объектами.
Например, граф, отражающий отношение «переписываются» между объектами класса «дети», может выглядеть, как показано на рис. 44.
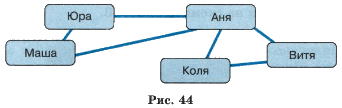
Отношение «переписываются» («пишут письма друг другу») является двухсторонним (симметричным). Поэтому соответствующие вершины соединены линиями без стрелок (рёбрами).
Граф называется неориентированным, если его вершины соединены ребрами.
Путь по вершинам и рёбрам графа, включающий любое ребро графа не более одного раза, называется цепью.
Пример цепи: Юра — Аня — Витя — Коля (см. рис. 44).
Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Пример цикла: Аня — Коля — Витя — Аня.
Иначе выглядит граф, отражающий отношение «пишет письма» между теми же объектами класса «дети». Линии со стрелками (дуги) придают ему совершенно иной смысл (рис. 45).
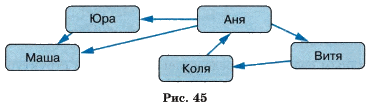
Граф называется ориентированным, если его вершины соединены дугами.
Приведите примеры цепи и цикла в графе на рис. 45.
Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).
На рисунке 46 информация о городах Золотого кольца представлена взвешенным графом: веса его вершин — года основания городов, веса рёбер — расстояния в километрах между городами.
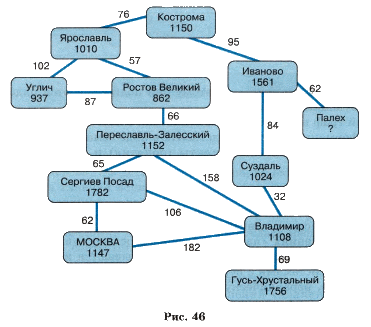
Назовите пути и циклы в графе на рис. 46.
Граф с циклами называется сетью.
На рисунке 47 в виде графа представлена информационная модель сказки про Царевну-лягушку.
Вершины этого графа — персонажи и предметы из сказки, дуги — связи между ними. В отличие от предыдущих примеров,
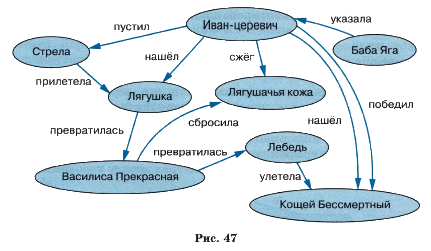
здесь все связи различны. Поэтому они подписываются рядом с соответствующими дугами.
Такой граф называется семантической сетью. Считается, что любую информацию можно представить в виде семантической сети, на которой будут отражены объекты (понятия) и связи (отношения) между ними.


