Урок 22
Информационные модели на графах
Использование графов при решении задач
Практическая работа №14
«Создаём информационные модели – схемы, графы, деревья» (задания 4 и 6)
Содержание урока
Информационные модели на графах
Использование графов при решении задач
Компьютерный практикум. Ресурсы ЕК ЦОР. Задания 1 - 7
Использование графов при решении задач
Графы удобно использовать при решении некоторых классов задач.
Задача 1
Сколькими способами можно рассадить в ряд на три стула трёх учеников? Выписать все возможные случаи.
Решение этой задачи удобнее всего представить в виде дерева. За его корневую вершину возьмём произвольную точку плоскости О.
На первый стул можно посадить любого из трёх учеников — обозначим их А, В л С. На схеме это соответствует трём ветвям, исходящим из точки О (рис. 51).
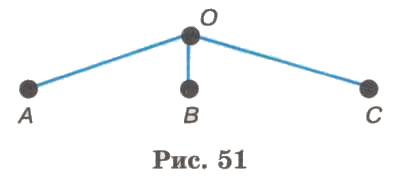
Посадив на первый стул ученика А, на второй стул можно посадить ученика В или С. Если же на первый стул сядет ученик В, то на второй можно посадить А или С. Если на первый стул сядет С, то на второй можно будет посадить А или В. Это соответствует на схеме двум ветвям, исходящим из каждой вершины первого уровня (рис. 52).
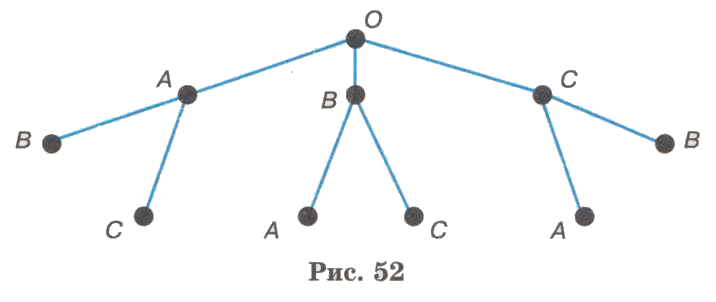
Очевидно, что третий стул в каждом случае займёт оставшийся ученик. Это соответствует одной ветви дерева, которая «вырастает» на каждой из предыдущих ветвей (рис. 53).
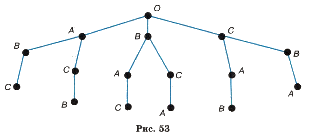
Выпишем все пути от вершин первого уровня к вершинам третьего уровня: А-В-Су А-С-В, В-А-С, В-С-А, С-А-Б, С-В-А. Каждый из выписанных путей определяет один из вариантов рассаживания учеников на стулья. Так как других путей нет, то искомое число способов — 6.
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их число. В этом случае рассуждать нужно так: на первый стул можно усадить одного из трёх человек, на второй — одного из двух оставшихся, на третий — одного оставшегося: 3-2-1 = 6.
Задача 2
Чтобы принести Царю-батюшке молодильные яблоки, должен Иван-царевич найти единственный верный путь к волшебному саду. Встретил Иван-царевич на развилке трёх дорог старого ворона и вот какие советы от него услышал:
1) иди сейчас по правой тропинке;
2) на следующей развилке не выбирай правую тропинку;
3) на третьей развилке не ходи по левой тропинке.
Пролетавший мимо голубь шепнул Ивану-царевичу, что только один совет ворона верный и что обязательно надо пройти по тропинкам разных направлений. Наш герой выполнил задание и попал в волшебный сад. Каким маршрутом он воспользовался?
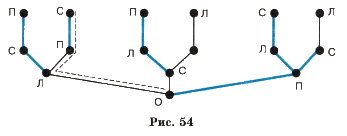
Обозначим левую, среднюю и правую тропинки соответственно Л, С и П. Возможные маршруты представим в виде графа. При этом подсказки ворона отметим более «жирными» рёбрами. Так как только один совет ворона верен, то на графе ему будет соответствовать маршрут, имеющий одно «жирное» ребро. Этот маршрут обозначен дополнительной пунктирной линией (рис. 54).