Уроки 35 - 39
Формальные исполнители
§ 30. Способы записи алгоритмов
§ 31. Примеры исполнителей
§32. Оптимальные программы
Содержание урока
§ 30. Способы записи алгоритмов
§ 31. Примеры исполнителей
§32. Оптимальные программы
Задача
Задача
Ключевые слова:
• оптимальная программа • дерево вариантов
Задача. В системе команд исполнителя Удвоитель всего две команды:
1. прибавь 1
2. умножь на 2
Составьте самую короткую программу для Удвоителя, которая преобразует число 6 в 28.
Попытайтесь решить задачу самостоятельно. Сравните своё решение с решениями одноклассников. У кого получилось короче?
Возможно, в этой простой задаче вы сразу сообразили, какой будет самая короткая программа. Но в более сложных случаях это не так просто. Кроме того, нужно доказать, что это действительно самая короткая программа. Поэтому рассмотрим общий способ решения. Самую короткую программу можно назвать оптимальной по длине.
 Оптимальная программа — это самая лучшая программа по какому-то показателю.
Оптимальная программа — это самая лучшая программа по какому-то показателю.
В этой задаче нас интересует программа, содержащая меньше всего команд.
За одну команду мы можем из начального числа 6 получить только число 7 (командой 1) или число 12 (командой 2) — рис. 6.8.
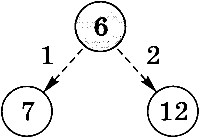
Рис. 6.8
Выясните, какие числа можно получить с помощью Удвоителя из начального числа 6 за два шага.
Проверим все возможные трёхшаговые программы. Мы обнаружим, что одна из программ, 122 (она выделена голубыми стрелками на рис. 6.9), приведёт к нужному нам значению 28.
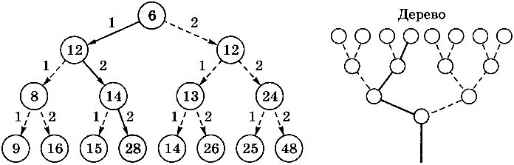
Рис. 6.9
Следующая страница  Дерево возможных вариантов
Дерево возможных вариантов

