Уроки 35 - 39
Формальные исполнители
§ 30. Способы записи алгоритмов
§ 31. Примеры исполнителей
§32. Оптимальные программы
Содержание урока
§ 30. Способы записи алгоритмов
§ 31. Примеры исполнителей
§32. Оптимальные программы
Дерево возможных вариантов
Дерево возможных вариантов
До этого вы убедились, что за одну и даже за две команды число 28 получить невозможно, поэтому программа 122 из трёх команд — оптимальная, т. е. самая короткая.
Как видно из рис. 6.9, нет других программ из трёх команд, которые приводят к числу 28, поэтому оптимальная программа единственная. Все другие программы, с помощью которых можно получить число 28 из 6, длиннее, чем эта.
Схема, которую мы построили, называется деревом возможных вариантов. Действительно, мы рассмотрели все возможные программы, состоящие из одного, двух и трёх шагов. Если полученный рисунок развернуть «вверх ногами», он напоминает дерево (рис. 6.9, справа).
Построение полного дерева вариантов при большой длине программы (например, 5 и больше команд) — это очень утомительная работа. Во многих задачах бывает проще двигаться не от начального числа к результату, а наоборот.
Можно ли составить программу, которая на последнем шаге получает число 28 командой 1? Командой 2? Что можно сказать про число 27?
Возьмём конечное число 28 и подумаем, какой последней командой мы могли его получить. Так как 28 делится на 2, это могла быть как команда 1 (из 27 получаем 28), так и команда 2 (из 14 также получаем 28). Ни одно из этих чисел не совпадает с начальным (6), поэтому одной командой задачу не решить.
Делаем второй шаг — проверяем, из каких чисел мы могли получить 27 и 14. Число 27 не делится на 2, поэтому оно могло быть получено только командой 1 (из 26), а число 14 можно получить из 13 или из 7 (рис. 6.10).
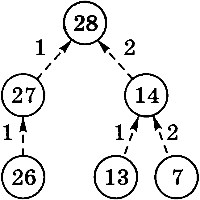
Рис. 6.10
До начального числа 6 снова добраться не удалось, поэтому решений из двух команд не существует. Делаем третий шаг (рис. 6.11).
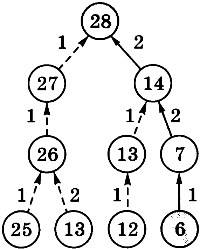
Рис. 6.11
Для того чтобы получить самую короткую программу, нужно пройти по стрелкам от начального числа к конечному, выписывая встречающиеся номера команд. Для нашей задачи получаем тот же ответ, что и раньше, — 122 (путь выделен голубыми стрелками).
Обратите внимание, что дерево при движении в обратном направлении, от конечного числа к начальному, получилось меньше. Нам удалось найти решение быстрее, рассматривая меньше вариантов.
Объясните, почему в некоторых случаях в дереве на рис. 6.11 не было разделения на две ветки.
Следующая страница  Выводы. Интеллект-карта
Выводы. Интеллект-карта

