Урок 3
§5. Дискретное кодирование

Содержание урока

Дискретизация

Равномерные коды

Неравномерные коды

Код Морзе

Измерение количества информации

Выводы. Интеллект-карта

Вопросы и задания

Проекты

Равномерные коды

Если нам нужно записать в память компьютера какой-то текст на русском языке, его нужно представить в виде двоичного кода, т. е. перекодировать.

Например, перекодируем слово ГАГАРА в двоичный алфавит, считая, что в тексте есть только буквы «А», «Г» и «Р», т. е. алфавит состоит из трёх знаков. Присвоим каждой из этих букв двоичные коды — кодовые слова (рис. 2.5).

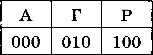
Рис. 2.5

Закодируйте с помощью этого кода слово ГАГАРА.

Такой код называется равномерным, потому что длина всех кодовых слов одинакова.

Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.

Теперь предположим, что по компьютерной сети передана цепочка

000010000100000010000100

Известно, что для кодирования использовалась таблица, показанная на рис. 2.5, и нам нужно узнать, какое сообщение было закодировано. Эта операция называется декодированием.

Декодирование — это восстановление исходного сообщения из кода.

Сообщение 000010000100000010000100 закодировано с помощью равномерного кода, приведённого на рис. 2.5. Определите, сколько знаков было в исходном сообщении. Как вы рассуждали? Декодируйте это сообщение.

Равномерный 5-битный двоичный код, разработанный в конце XIX века Жаном Морисом Бодо, использовался в телеграфных аппаратах. В современных компьютерных системах при передаче текстовых сообщений также часто применяют равномерный (8-битный или 16-битный) код.

Можно ли было для кодирования букв «А», «Г», «Р» использовать более короткий равномерный код? Определите наименьшую возможную длину кодовых слов.

Если для кодирования используется алфавит мощностью M, то с помощью кодовых слов длиной L можно закодировать M^L различных знаков. Это число должно быть не меньше, чем мощность алфавита исходного сообщения M₀, потому что иначе какие-то буквы обязательно получат одинаковые коды.

Длину кодовых слов L выбирают из условия M^L ≥ M₀, где М₀ — мощность алфавита исходного сообщения и М — мощность нового алфавита.

Как выбрать наименьшую возможную длину кодовых слов при равномерном кодировании?

В сообщении используются 33 русские прописные буквы и пробел. Определите наименьшую длину кодовых слов для равномерного кодирования этого сообщения в трёхбуквенном и четырёхбуквенном алфавитах.

Следующая страница Неравномерные коды

Cкачать материалы урока