Урок 33
Итоговое тестирование

Задания для итогового тестирования будут взяты из вопросов контрольных работ:
1 Контрольная работа № 1 "СИСТЕМЫ СЧИСЛЕНИЯ"
2 Контрольная работа № 2 "ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ"
3 Контрольная работа № 3 "МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ"
4 Контрольная работа № 4 "АЛГОРИТМЫ И ИСПОЛНИТЕЛИ"
5 Разноуровневая контрольная работа № 5 "НАЧАЛА ПРОГРАММИРОВАНИЯ"

Контрольная работа № 4 "АЛГОРИТМЫ И ИСПОЛНИТЕЛИ"

ВАРИАНТ 1

1. У исполнителя Вычислитель две команды, которым присвоены номера: 1 — умножь на 3; 2 — вычти 3.

Первая из них увеличивает число в 3 раза, вторая уменьшает его на 2. Составьте алгоритм получения из числа 5 числа 60, содержащий не более пяти команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

2. Чертёжнику был дан для исполнения следующий алгоритм:

Какой должна быть Команда 1, чтобы Чертёжник вернулся в исходную точку, из которой он начал движение?

3. Цепочка из четырёх бусин, помеченных латинскими буквами, формируется по следующему правилу:

1) в начале — одна из бусин В, С, D, которой нет на четвёртом месте;
2) на втором месте цепочки стоит одна из бусин В, А, Е;
3) на третьем месте — одна из бусин Е, С, D, не стоящая на первом месте;
4) в конце — одна из бусин А, С, Е, которой нет на втором месте.

Определите, сколько из перечисленных ниже цепочек созданы по этому правилу.

ВЕСС CEDC CAED DEEC АВСЕ BBDA DBDC DBAE ВАЕА

4. Определите значение переменной а после исполнения следующего алгоритма.

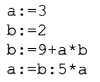
Порядок действий соответствует правилам арифметики.

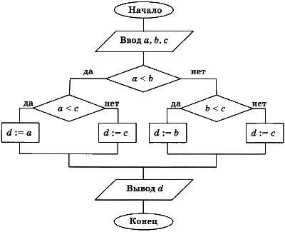
5. Определите значение переменной d после исполнения следующего алгоритма, если переменным а, b, с были присвоены значения 10, 12 и 100 соответственно.

6. Запишите значение переменной s, полученное в результате выполнения следующего алгоритма.

7. На бесконечном клетчатом поле находится длинная горизонтальная стена. Длина стены неизвестна. Робот (обозначен буквой «Р») находится в закрашенной клетке над стеной.

Робот должен закрасить все клетки, прилегающие к горизонтальной стене сверху (так, как это изображено на рисунке ниже). Конечное положение Робота значения не имеет.

8. Дополнительное задание. К четырёхзначному натуральному числу, все цифры которого различны, применяется следующий алгоритм.

1) Найти сумму трёх самых больших по значению цифр числа.
2) Вычесть из полученной суммы наименьшую по значению цифру числа.
Пример работы алгоритма для числа 3148:

3 + 4 + 8 = 15, 15 - 1 = 14.

Укажите наименьшее четырёхзначное число, все цифры которого различны, такое что в результате применения к нему данного алгоритма получится число 16.

ВАРИАНТ 2

1. У исполнителя Вычислитель две команды, которым присвоены номера: 1 — умножь на 5; 2 — вычти 5.

Первая из них увеличивает число в 5 раз, вторая уменьшает его на 5. Составьте алгоритм получения из числа 4 числа 80, содержащий не более пяти команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

2. Чертёжнику был дан для исполнения следующий алгоритм:

Какой должна быть Команда 1, чтобы Чертёжник вернулся в исходную точку, из которой он начал движение?

3. Автомат получает на вход пятизначное десятичное число. По полученному числу строится новое десятичное число по следующему правилу.

1) Вычисляются два числа — сумма первой, третьей и пятой цифр и сумма второй и четвёртой цифр заданного числа.
2) Полученные два числа записываются друг за другом в порядке неубывания (без разделителей).

Пример: исходное число: 14351. Поразрядные суммы: 5, 9. Результат: 95.

Определите, сколько из приведённых ниже чисел может получиться в результате работы автомата.

30 1528 116 1519 2019 1920 1915 316 2815

4. Определите значение переменной а после исполнения следующего алгоритма.

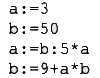
Порядок действий соответствует правилам арифметики. Ответ:

5. Определите значение переменной d после исполнения следующего алгоритма, если переменным а, b, с были присвоены значения 100, 12 и 100 соответственно.

6. Запишите значение переменной s, полученное в результате выполнения следующего алгоритма.

7. На бесконечном клетчатом поле находится длинная горизонтальная стена. Длина стены неизвестна. Робот (обозначен буквой «Р») находится в закрашенной клетке под стеной.

Робот должен закрасить все клетки, прилегающие к горизонтальной стене снизу (так, как это изображено на рисунке ниже). Конечное положение Робота значения не имеет.

8. Дополнительное задание. К пятизначному нечётному натуральному числу применяется следующий алгоритм.

1) Записать цифры исходного числа в обратном порядке.
2) Сложить получившееся число с исходным числом. Пример работы алгоритма для числа 22011:

22011 + 11022 = 33033.

Укажите наибольшее пятизначное нечётное число, в результате применения к которому данного алгоритма получится число 65856.

Электронное приложение к уроку

Cкачать материалы урока