Уроки 13 - 14
§17. Графы
Содержание урока
Взвешенный граф
Взвешенный граф
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).
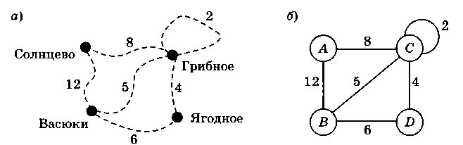
Рис. 3.22
 Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).
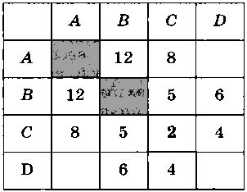
Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?
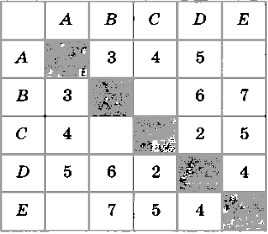
Рис. 3.24
Следующая страница  Оптимальный путь в графе
Оптимальный путь в графе

