Уроки 13 - 14
§17. Графы
Содержание урока
Оптимальный путь в графе
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).
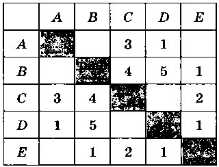
Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую
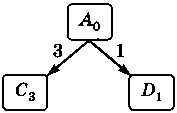
Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).
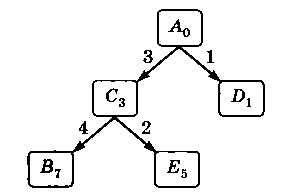
Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28
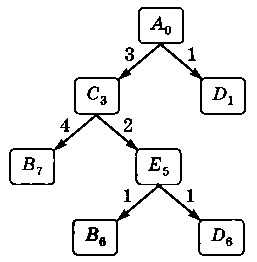
Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).
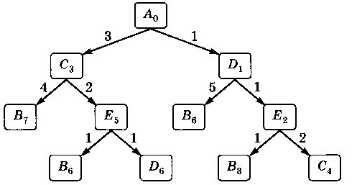
Рис. 3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Следующая страница  Ориентированный граф
Ориентированный граф

