Уроки 25 - 26
§16. Списки и деревья
Содержание урока
Где используются деревья?
Где используются деревья?
Типичный пример иерархии — различные классификации (животных, растений, минералов, химических соединений). Например, отряд Хищные делится на два подотряда: Псообразные и Кошкообразные. В каждом из них выделяют несколько семейств (рис. 3.11).
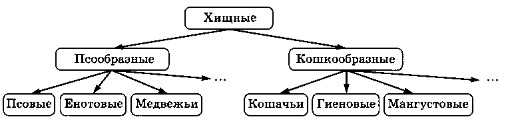
Рис. 3.11
Конечно, на этой схеме показаны не все семейства, остальные обозначены многоточием.
В текстах иерархию часто представляют в виде многоуровневого списка. Например, оглавление книги о хищниках может выглядеть так:
Глава 1. Псообразные
Псовые
Енотовые
Медвежьи
Глава 2. Кошкоообразные
2.1 Кошачьи
2.2 Гиеновые
2.3 Мангустовые
Работая с файлами и папками, мы тоже встречаемся с иерархией: классическая файловая система имеет древовидную структуру 1). Вход в папку — это переход на следующий (более низкий) уровень иерархии (рис. 3.12).
1) В некоторых файловых системах файл может «принадлежать» нескольким папкам одновременно. При этом древовидная структура, строго говоря, нарушается.
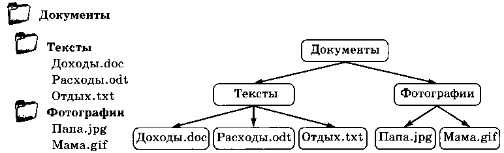
Рис. 3.12
Запишите по схеме на рис. 3.12 полный адрес файла Расходы.odt. Если вы работаете в операционной системе Windows, считайте, что папка Документы находится в корневой папке диска С:, для системы Linux — в папке /home/sonya.
Алгоритм вычисления арифметического выражения может быть представлен в виде модели-дерева (рис. 3.13).
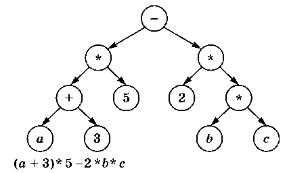
Рис. 3.13
Здесь листья — это числа и переменные, а корень и промежуточные узлы — знаки операций. Вычисления выполняются «снизу вверх» — от листьев — к корню.
Представление арифметического выражения в виде дерева позволяет выделить независимые друга от друга операции, которые современные процессоры могут выполнять одновременно (или, как говорят, параллельно). Например, на рис. 3.14 видно, что умножение b • с никак не зависит от сложения a + 3. Если считать, что время выполнения всех операций одинаково и равно T, то процессор, имеющий несколько устройств для выполнения арифметических операций, вычислит это выражение за время 3Т вместо 5Т.
В дереве для вычисления арифметического выражения (см. рис. 3.13) каждый узел может иметь не более двух сыновей, поэтому оно называется двоичным (или бинарным). От расположения сыновей зависит результат вычитания и деления, поэтому используют термины «левый сын» и «правый сын», «левое поддерево» и «правое поддерево».
Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «бинарный».
Постройте дерево, соответствующее арифметическому выражению (5*b+а)/(2*а+3*b+6).
Следующая страница 
Перебор вариантов
Cкачать материалы урока
