Уроки 25 - 26
§16. Списки и деревья
Содержание урока
Перебор вариантов
Перебор вариантов
С помощью дерева можно изобразить многошаговый процесс, в котором на каждом шаге делается выбор из нескольких вариантов. Например, русские богатыри в сказках часто выбирали на развилке, куда поехать — налево, прямо или направо. В игре «крестики-нолики» каждый игрок на каждом ходу тоже выбирает один из всех возможных вариантов.
Например, построим все двухбуквенные слова, которые можно записать с помощью алфавита {А, Б, В}. Начнём с пустого слова, в котором нет ни одной буквы (на рис. 3.14 оно изображено чёрным кружком в корне дерева), и будем на каждом шаге добавлять в конец слова одну из трёх возможных букв (см. рис. 3.14).
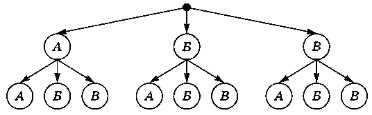
Рис. 3.14
Чтобы найти само слово, нужно выписать метки всех узлов на пути от корня до листа. Например, узлы, выделенные серым фоном на рис. 3.14, соответствуют слову БВ.
Можно рисовать это дерево иначе, повернув его на бок. В § 15 такая запись использовалась при выборе оптимального маршрута.
Разведчик выяснил, что ключ к замку от сейфа состоит из трёх символов, причём могут использоваться буквы из алфавита {А, В, С, D}. Две одинаковые буквы не могут стоять рядом. Рядом с буквой D обязательно должна стоять буква А. Если в ключе есть буква В, то там не может быть буквы С. Постройте дерево перебора вариантов и подсчитайте, сколько различных ключей удовлетворяют этим условиям.
Следующая страница  Дерево для двоичного кода
Дерево для двоичного кода

