Урок 51
§28. Численные методы
Содержание урока
Что такое численные методы?
Решение уравнений подбором параметра
Практическая работа № 29 «Решение уравнений»
Что такое численные методы?
Ключевые слова:
• аналитическое решение • численный метод • приближённое решение • приближённый метод • начальное приближение • итерационный метод • подбор параметра • целевая ячейка • изменяемая ячейка
На уроках математики вас учили искать решение уравнения в виде формулы, выражающей неизвестную величину через известные. Например, решение уравнения ах + b = 1 при а ≠ 0 можно записать в виде х = (1 - Ь)/а. Такое решение называется аналитическим, оно может быть использовано для теоретического исследования (изучения влияния исходных данных на результат).
Пусть а > 0, 6 < 1 и х = (1- b)/а. Как при этом изменится значение х, если
а) увеличить а, не изменяя 6;
б) уменьшить 6, не изменяя а?
Однако не все уравнения можно на современном уровне развития математики решить аналитически. Иногда решение есть, но очень сложное. Часто значительно легче получить численное решение, т. е. найти число, которое является решением при конкретных исходных данных (а не формулу!).
 Численное решение — это решение задачи для конкретных исходных данных.
Численное решение — это решение задачи для конкретных исходных данных.
 Численный метод — это метод, который применяется для поиска численного решения.
Численный метод — это метод, который применяется для поиска численного решения.
Как правило, численные методы дают не точное, а приближённое решение, т. е. решение с некоторой ошибкой. Если эта ошибка будет достаточно мала (например, при вычислении расстояния между городами ошибка составит не более 1 м), то такое решение всех устроит.
 Приближённый метод — это метод, который позволяет найти решение задачи с некоторой (допустимой) ошибкой (погрешностью).
Приближённый метод — это метод, который позволяет найти решение задачи с некоторой (допустимой) ошибкой (погрешностью).
 Погрешность — отклонение значения величины, полученного в результате измерений или вычислений, от её истинного (действительного) значения.
Погрешность — отклонение значения величины, полученного в результате измерений или вычислений, от её истинного (действительного) значения.
Рассмотрим уравнение х = cos х, для которого решение в виде формулы получить нельзя.
Как бы вы решали такое уравнение, если бы его очень нужно было решить?
В этом случае можно использовать, например, графический метод решения: построить по точкам графики функций, стоящих в левой и правой частях равенства, и посмотреть, где они пересекаются. В точке пересечения значения функций равны, значит, соответствующее значение х — это решение уравнения (рис. 5.13). Решение можно уточнять, уменьшая шаг построения графика до получения требуемой точности.
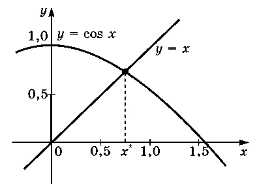
Рис. 5.13
Если нужна высокая точность, графический метод требует очень большого объёма вычислений, который можно поручить компьютеру. Однако нужно как-то учесть, что компьютер не способен «посмотреть» на график, и для уточнения решения может использовать только числовые данные. Компьютерный алгоритм решения уравнения может выглядеть примерно так:
1) выбрать отрезок [а0; b0] для поиска решения (обычно предполагается, что на этом отрезке есть решение, и притом только одно);
2) с помощью некоторого алгоритма уточнить решение, перейдя к меньшему отрезку [а, b];
3) повторять шаг 2, пока длина отрезка, в который мы «загнали» решение, не станет достаточно малой.
Здесь не совсем ясно, что значит «пока длина отрезка не станет достаточно малой». Обычно задаётся допустимая погрешность ε: отклонение полученного решения от истинного х не должно быть больше, чем ε. Когда мы уменьшаем отрезок, внутри которого находится решение, мы увеличиваем точность: при выборе любой точки этого отрезка в качестве решения ошибка не превышает длины отрезка.
Установлено, что корень уравнения находится на отрезке [а, b]. Какую точку этого отрезка лучше всего считать решением? Какова будет в этом случае наибольшая возможная погрешность?
Цикл (повторение шага 2 алгоритма) нужно остановить тогда, когда длина отрезка станет меньше, чем 2ε. В этом случае при выборе х = (а + b)/2 погрешность будет минимальной: не больше, чем ε.
Часто используется другой вариант, когда требуется знать только одну точку вблизи решения — начальное приближение.
 Начальное приближение — это начальное значение неизвестной величины, которое уточняется с помощью приближённого метода.
Начальное приближение — это начальное значение неизвестной величины, которое уточняется с помощью приближённого метода.
Процедуры уточнения (они бывают разные!) работают примерно так:
1) выбрать начальное приближение х0 около решения;
2) с помощью некоторого алгоритма перейти к следующему приближению х, которое находится ближе к точному решению х*;
3) повторять шаг 2, пока изменение значения х не станет меньше, чем допустимая погрешность ε.
При каждом уточнении повторяются одинаковые действия, поэтому такие методы называют итерационными.
Вспомните, что означает слово «итерация».
Приближённые методы имеют ряд недостатков:
• получается приближённое решение, а не точное; это значит, что нельзя написать х* = 1,2345, нужно использовать знак приближённого равенства: х* ≈ 1,2345;
• мы получаем не формулу, а число, по которому невозможно оценить, как меняется решение при изменении исходных данных (сложно выявить зависимость от параметра);
• объём вычислений может быть слишком велик, это не позволяет использовать приближённые методы в системах, где нужно очень быстро получить результат;
• не всегда можно оценить погрешность (ошибку) результата.
Однако в реальных задачах очень часто аналитическое решение получить невозможно или очень трудно, а приближённые методы позволяют быстро решить задачу с заданной точностью.
Следующая страница  Решение уравнений подбором параметра
Решение уравнений подбором параметра

