Урок 51
§28. Численные методы

Содержание урока

Что такое численные методы?

Решение уравнений подбором параметра

Выводы

Вопросы и задания

Практическая работа № 29 «Решение уравнений»

Решение уравнений подбором параметра

Для решения уравнений можно использовать табличный процессор, например OpenOffice Calc (или LibreOffice Calc) или Microsoft Excel. Обычно сначала строится график функции, по которому определяют количество корней уравнения и их примерное расположение; затем используется команда Подбор параметра. Далее мы будем рассматривать программу Calc из пакета OpenOffice, указывая на незначительные отличия Excel.

Найдём все решения уравнения х² = cos х на отрезке [-2; 2]. Сначала определим, сколько решений имеет это уравнение. Для этого построим графики обеих функций: f₁(x) = х² и f₂(х) = cos х. Составим таблицу, где значения х расположены в столбце А, значения функций — в столбцах В и С. Выберем шаг изменения х, равный 0,25.

Можно ли выбрать другой шаг? Что изменится (улучшится, ухудшится), если увеличивать шаг? Уменьшать шаг?

Введём два первых значения х в столбце А, выделим их и «протащим» маркер заполнения вниз до тех пор, пока последнее значение в столбце А не станет равно 2 (рис. 5.14).

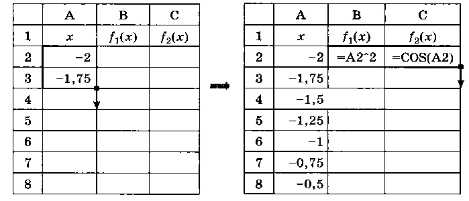
Рис. 5.14

Введём в ячейки В2 и С2 формулы, вычисляющие значения обеих функций для значения х в ячейке А2. Затем выделим формулы и скопируем их вниз до конца таблицы (например, сделав двойной щелчок на маркере заполнения).

Теперь выделяем все данные и строим диаграмму типа Диаграмма X-Y (Точечная) — рис. 5.15.

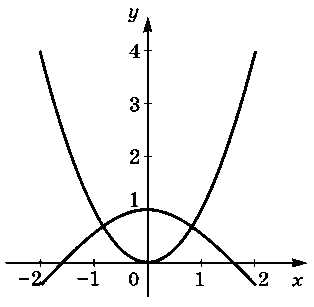
Рис. 5.15

Изучите график на рис. 5.15. Сколько решений имеет уравнение на этом отрезке? Найдите начальные приближения для поиска всех решений — значения х, расположенные рядом с решениями.

Найдём решение вблизи точки х = - 1. В отдельных ячейках (чтобы не портить графики!) введём начальное приближение и вычислим значения обеих функций (в ячейках F2 и G2). Кроме того, в Н2 запишем формулу для вычисления разности значений функций (рис. 5.16).

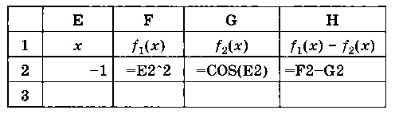
Рис. 5.16

Чему должна быть равна разность двух функций в точке х, которая является решением уравнения?

Табличные процессоры умеют решать задачу подбора параметра, которая формулируется так: установить в ячейке X значение V, изменяя значение ячейки Y. Например, в нашем случае нужно установить в ячейке Н2 значение 0, изменяя Е2. Ячейка Н2 называется целевой, потому что наша цель — получить в ней определённое значение (ноль). Ячейка Е2, значение которой мы хотим подобрать, — это изменяемая ячейка.

В главном меню выбираем пункт Сервис → Подбор параметра¹⁾ и вводим эти данные (рис. 5.17):

---

¹⁾ В программе Excel — пункт Подбор параметра в группе Анализ что-если на вкладке Данные.

---

Рис. 5.17

После нажатия на кнопку ОК найденное решение уравнения будет записано в ячейку Е2.

Как же найти второе решение? Для этого нужно выбрать другое начальное приближение, например х = 1. В остальном порядок действий не меняется.

Можно ли вместо уравнения х² = cos х решать уравнение х² - cos х = 0? Чем лучше такой подход?

Следующая страница Выводы

Cкачать материалы урока