Уроки 46 - 47
Сочетание циклов и ветвлений. Алгоритм Евклида
(§ 16. Алгоритм Евклида)
Использование алгоритма Евклида при решении задач

Содержание урока

Алгоритм Евклида

Дополнительный материал к главе II (§§ 8 - 21). Сложность алгоритмов

Компьютерный практикум ЦОР. Алгоритм Евклида (Задание 1 - 5)

Компьютерный практикум ЦОР. Алгоритм Евклида (Задание 6 - 11)

Алгоритм Евклида

Наибольший общий делитель

Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.

Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они оба делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:

НОД(12, 18) = 6. 

Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:

Дано: М, N.

Найти: НОД(М, N).

В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.

Идея алгоритма Евклида

Идея этого алгоритма основана на том свойстве, что если M > N, то

НОД(М, N) = НОД(М - N, N).

Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.

Легко доказать это свойство. Пусть К — общий делитель М и N (М > N). Это значит, что М = mК, N = nК, где m, n — натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К — делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N, в том числе и наибольший общий делитель.

Второе очевидное свойство:

НОД(М, М) = М.

Для «ручного» счета алгоритм Евклида выглядит так:

1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;

2) заменить большее число разностью большего и меньшего из чисел;

3) вернуться к выполнению п. 1.

Рассмотрим этот алгоритм на примере М=32, N=24:

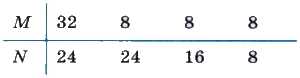
Получили: НОД(32, 24) = НОД(8, 8) = 8, что верно.

Описание алгоритма Евклида блок-схемой

На рисунке 2.8 приведена блок-схема алгоритма Евклида.

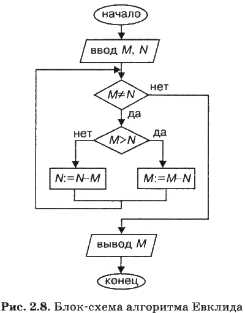
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.

А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24: 

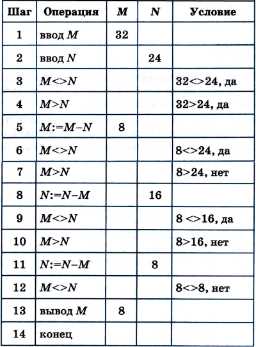
В итоге получился верный результат.

Коротко о главном

Алгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением.

Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Поиск алгоритмических ошибок в программе производится с помощью тестирования.

Вопросы и задания

1. Выполните на компьютере программу Evklid (из параграфа). Протестируйте ее на значениях М = 32, N = 24; М = 696, N = 234.

2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:

НОД(А, В, С) * НОД(НОД(А, В), С).

3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:

А * В = НОД(А, В)-НОК(А, В).