Уроки 46 - 47
Сочетание циклов и ветвлений. Алгоритм Евклида
(§ 16. Алгоритм Евклида)
Использование алгоритма Евклида при решении задач
Содержание урока
Дополнительный материал к главе II (§§ 8 - 21). Сложность алгоритмов
Компьютерный практикум ЦОР. Алгоритм Евклида (Задание 1 - 5)
Компьютерный практикум ЦОР. Алгоритм Евклида (Задание 6 - 11)
Дополнительный материал к главе II (§§ 8 - 21)
Сложность алгоритмов
Традиционно принято оценивать степень сложности алгоритма по объему используемых им основных ресурсов компьютера: процессорного времени и оперативной памяти. В связи с этим вводятся такие понятия, как временная сложность и объемная сложность алгоритма.
Объемная сложность связана с количеством данных, которые при обработке нужно хранить в оперативной памяти. Проблемы могут возникнуть при обработке больших массивов данных (числовых или символьных). Если весь объем обрабатываемой информации не помещается одновременно в оперативную память, то эти данные приходится хранить на устройствах внешней памяти (дисках) и в процессе обработки перемещать частями из внешней памяти в оперативную память и обратно. Поскольку время чтения и записи данных на устройствах внешней памяти намного больше времени обмена процессора с оперативной памятью, то в целом время выполнения программы существенно возрастает.
Временная сложность связана с количеством операций, выполняемых процессором в течение работы программы. Наибольшая часть процессорного времени тратится на выполнение циклов. Поэтому оценка временной сложности производится по количеству повторений циклов. Нетрудно понять, что при обработке массива данных количество повторений циклов связано с размером массива. Например, пусть вычисляется сумма элементов массива X, состоящего из N чисел:
S:=0; for i:=1 to N do S:=S + X[±];
В теле цикла выполняется две операции: сложение и присваивание. Число повторений цикла равно N. Следовательно, суммарное число выполняемых операций равно N • 2. Значит, время выполнения всего цикла будет пропорционально N • 2: Т ~ N • 2. В таком случае говорят, что временная сложность алгоритма зависит линейно от объема данных. Во сколько раз возрастет N, во столько же раз возрастет время выполнения программы.
Если вернуться к алгоритму поиска наибольшего и наименьшего значений массива, то в нем также имеется один цикл, хотя тело цикла содержит большее число операций. Но с увеличением размера массива (N) время выполнения программы будет также увеличиваться линейно, т. е. пропорционально N. Следовательно, временная сложность алгоритмов суммирования массива и поиска в массиве максимального (минимального) элемента одинаковая — линейная.
Теперь оценим временную сложность алгоритма сортировки массива методом пузырька. По-прежнему обозначим через N размер массива. Алгоритм содержит два вложенных цикла. Внешний цикл имеет длину N - 1. Внутренний цикл с каждым повторением изменяет свою длину по убыванию: N - 1, N - 2, N - 3, ..., 2, 1. Суммарное число повторений цикла можно посчитать так:
• вычислим среднюю длину внутреннего цикла:
[(N- 1)+ 1]/2 = N/2 ;
• умножим эту величину на число повторений внешнего цикла:
(N - 1) • N/2 = (N2 - N)/2.
Временная сложность алгоритма определяется слагаемым с наибольшей степенью: Т ~ N2. В таком случае говорят, что временная сложность алгоритма сортировки методом пузырька имеет второй порядок по объему данных, т. е. пропорциональна квадрату N. Например, если размер массива увеличить в 10 раз, то время сортировки возрастет в 100 раз.
Сложность алгоритмов перебора
Большим классом задач, которые часто решаются на компьютере, являются задачи поиска. Одну из таких задач мы уже рассматривали: поиск максимального элемента в массиве. Общий смысл задач поиска сводится к следующему: из множества данных, хранящихся в памяти компьютера, требуется выбрать нужные данные, удовлетворяющие определенным условиям (критериям). Такой поиск осуществляется перебором всех элементов структуры данных и их проверкой на удовлетворение условию поиска. Перебор, при котором просматриваются все элементы структуры, называется полным перебором.
На примере алгоритма поиска максимального элемента мы знаем, что полный перебор элементов одномерного массива производится с помощью одного цикла, число повторений которого пропорционально размеру массива.
Рассмотрим другой пример. В одномерном массиве X заданы координаты N точек, произвольно расположенных на вещественной числовой оси. Точки пронумерованы. Их номера соответствуют номерам элементов в массиве X. Нужно определить пару точек, расстояние между которыми наибольшее.
Применяя метод перебора, эту задачу можно решать так: перебрать все пары точек из N данных и определить номера тех точек, расстояние между которыми наибольшее (наибольший модуль разности координат). Такой полный перебор реализуется через два вложенных цикла:

Но очевидно, что такое решение задачи нерационально. Здесь каждая пара точек будет просматриваться дважды, например при i =1, j = 2 и i = 2, j = 1. Для случая N = 100 циклы повторят выполнение 100 • 100 = 10 000 раз.
Выполнение программы ускорится, если исключить повторения. Исключить также следует и совпадения значений i и j. Для исключения повторений нужно в предыдущей программе изменить начало внутреннего цикла с 1 на i + 1. Программа примет вид:
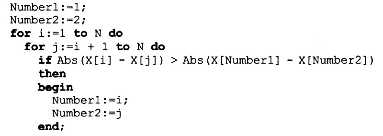
В таком алгоритме число повторений цикла будет равно N(N - 1)/2. При N = 100 получается 4950. Рассмотренный вариант алгоритма назовем перебором без повторений.
Замечание. Конечно, эту задачу можно было решить и другим способом, но в данном случае нас интересовал именно переборный алгоритм. В случае же точек, расположенных не на прямой, а на плоскости или в пространстве, поиск альтернативы переборному алгоритму становится весьма проблематичным.
В следующей задаче требуется выбрать из массива X без повторений все тройки чисел, сумма которых равна десяти. В этом случае алгоритм будет строиться из трех вложенных циклов. Внутренние циклы имеют переменную длину.
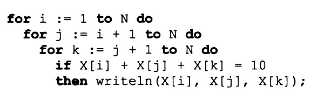
А теперь представьте, что из массива X требуется выбрать всевозможные группы чисел, сумма которых равна десяти. Количество чисел в группах может быть любым — от 1 до N. В этом случае количество вариантов перебора резко возрастает, а сам алгоритм становится нетривиальным.
Казалось бы, ну и что? Компьютер работает быстро! И все же посчитаем. Число различных групп из N объектов (включая пустую) составляет 2N. При N = 100 это будет 2100 ≈ 1030. Компьютер, работающий со скоростью миллиард операций в секунду, будет осуществлять такой перебор приблизительно 10 лет. Даже исключение перестановочных повторений не сделает такой переборный алгоритм практически осуществимым.
Путь практической разрешимости подобных задач состоит в нахождении способов исключения из перебора бесперспективных с точки зрения условия задачи вариантов. Для некоторых задач это удается сделать. К таким задачам относится задача поиска выхода из лабиринта, задача о восьми ферзях (расставить на шахматной доске восемь ферзей так, чтобы они не угрожали друг другу). Если бы шахматные программы составлялись методом полного перебора всевозможных ходов, то ни один суперкомпьютер не смог бы в реальном времени играть в шахматы. Очевидно, что в алгоритме программы заложены знания стратегии и тактики игры в шахматы, которыми владеют сильнейшие шахматисты, что существенно сокращает перебор возможных ходов.
Впечатляющим примером решения фундаментальной математической проблемы методом поиска является Проект GIMPS (Great Internet Mersenne Prime Search), направленный на поиск простых чисел Мерсенна — последовательности чисел, подчиняющихся закону 2Р-1, где р — простое число. В ноябре 2001 года в рамках данного проекта было найдено число Мерсенна, содержащее в своей десятичной записи более 4 млн цифр. Десятки тысяч компьютеров по всему миру, отдавая часть своих вычислительных ресурсов, работали над этой задачей два с половиной года.
Коротко о главном
В программировании используются два критерия сложности алгоритма: объемная сложность и временная сложность.
Объемная сложность связана с количеством данных, которые при обработке нужно хранить в оперативной памяти.
Временная сложность связана с количеством операций, выполняемых процессором в течение работы программы; количество операций пропорционально времени выполнения программы.
Временная сложность оценивается как функция зависимости числа операций от объема данных и может быть линейной, квадратичной и пр.
Задача перебора: из множества данных, хранящихся в памяти компьютера, требуется выбрать нужные данные, удовлетворяющие определенным условиям (критериям).
Временная сложность полного перебора может привести к превышению разумного времени выполнения программы на компьютере.
Оптимизация алгоритма перебора состоит в исключении анализа бесперспективных вариантов.
Вопросы и задания
1. Почему временная сложность алгоритма зависит от его объемной сложности?
2. Составьте алгоритм поиска для следующей задачи: на координатной плоскости заданы своими координатами N точек. Найти две самые удаленные друг от друга точки. Оцените временную сложность алгоритма. Рассмотрите два варианта алгоритма: с полным и с неполным перебором и сравните их.
3. Составьте алгоритм для решения задачи, аналогичной предыдущей, с учетом того что точки расположены в трехмерном пространстве.


