Уроки 21 - 24
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы
Содержание урока
§18. Логика и компьютер
§19. Логические операции
Логические выражения
§20. Диаграммы
§19. Логические операции
Логические выражения
Обозначив простые высказывания буквами (переменными) и используя логические операции, можно записать любое высказывание в виде логического выражения. Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолета. Обозначим высказывания:
А — «Первый двигатель вышел из строя».
В — «Второй двигатель вышел из строя».
С — «Третий двигатель вышел из строя».
X — «Аварийная ситуация».
Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):
X = (А • В) + (А • С) + (В • С). (2)
Здесь мы выполнили формализацию.
Формализация — это переход от конкретного содержания к формальной записи с помощью некоторого языка.
В логических выражениях операции выполняются в следующем порядке:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И);
4) логическое сложение (ИЛИ) и операция «исключающее ИЛИ»;
5) импликация;
6) эквивалентность.
Такой порядок означает, что все скобки в выражении (2) для X можно убрать. Порядок вычисления выражения можно, так же, как и для арифметических выражений, определить с помощью дерева (рис. 3.12). Вычисление начинается с листьев, корень — это самая последняя операция.
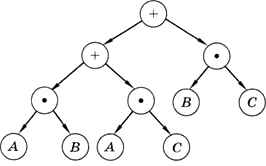
Рис. 3.12
Здесь каждая операция выполняется с двумя значениями. Такие операции называются бинарными (лат. bis — дважды) или двуместными.
Операции, которые выполняются над одной величиной, называют унарными (лат. ипо — один) или одноместными. Пример унарной логической операции — отрицание (операция «НЕ»).
Любую формулу можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Сложные выражения удобно разбить на несколько более простых, сначала вычислить значения этих промежуточных величин, а затем — окончательный результат.
Рассмотрим формулу (2). Выражение в правой части зависит от трёх переменных, поэтому существует 23 = 8 комбинаций их значений. Таблица истинности выглядит так, как показано на рис. 3.13.
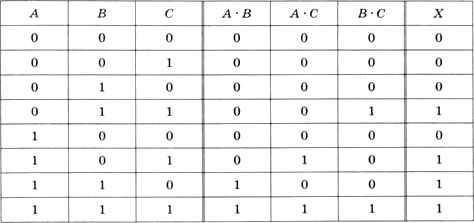
Рис. 3.13
По ней можно проверить, что выражение X истинно (возникает аварийная ситуация) тогда и только тогда, когда любые две (или все три) логические переменные А, В и С истинны (равны 1), т. е. любые два (или все три) двигателя вышли из строя. Поэтому формализация задачи выполнена верно.
Из таблицы 3.13 видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник, или он не учится в школе» всегда истинно (для любого Васи). Оно может быть записано в виде логического выражения А + А. Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение А • А всегда ложно, оно называется тождественно ложным или противоречием.
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Например, выражения А → В и А + В равносильны, равенство А → В и А + В называют тождеством. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Некоторые задачи
Рассмотрим ряд задач, в которых требуется исследовать логическое выражение.
Задача 1. Каково наибольшее целое число X, при котором истинно следующее высказывание?
А = (90 < Х2) → (80 > (Х + 2)2)
Сначала удобно заменить импликацию по формуле А → В = А + В. Отрицание для высказывания 90 < X2 запишется как 90 ≥ X2, поэтому
А=(90 ≥ Х2) или (80 > (Х + 2)2).
В этой задаче нас интересуют только целые числа. Поэтому условие 90 ≥ X2 можно заменить на (|Х| ≤ 9 или -9 ≤ X ≤ 9), а условие 80 > (Х + 2)2 — на (|Х + 2| ≤ 8 или 10 ≤ X ≤ 6). Таким образом, требуется выбрать наибольшее целое число, которое входит в один или в другой промежуток (рис. 3.14).
Рис. 3.14
Это число 9.
Задача 2. А, В и С — целые числа, для которых истинно высказывание
X = (А = В) • ((А > В) → (В > С)) • ((В > А) → (С > В)).
Чему равно В, если А = 27 и С = 25?
Данное сложное высказывание состоит из трёх простых:
(А = В), (А > В) → (В > С), (В > А) → (С > В).
Они связаны операцией «И», т. е. должны быть истинными одновременно. Из условия (А = В) = 1 сразу следует, что А ≠ В. Далее можно использовать несколько способов решения.
Способ 1 (решение «по частям»). Предположим, что А > В, тогда из второго условия получаем 1 → (В > С). Это выражение может быть истинно тогда и только тогда, когда (В > С) = 1, поэтому имеем А > В > С. Этому условию соответствует только число 26. Одно решение найдено.
Теперь проверим вариант А < В. Из второго условия получаем 0 → (В > С), это выражение истинно при любом В. Проверяем третье условие: получаем 1 → (С > В) = 1; это выражение может быть истинно тогда и только тогда, когда С > В, и тут мы получили противоречие, потому что нет такого числа В, для которого С > В > А. Таким образом, правильный ответ — 26, других решений нет.
Способ 2. Раскрываем импликацию через операции «ИЛИ» и «НЕ»:
(А > В) → (В > C) = (А > В) + (В > С) = (В ≥ А) + (В > C),
(В > А) → (С > В) = (В > А) + (С > В) = (В ≤ А) + (В < С).
Учитывая, что раньше мы выяснили, что А ≠ В, можно заменить знаки ≥ и ≤ соответственно на > и <. Подставляя значения А = 27 и С = 25, упрощаем выражения:
(В > 27) + (В > 25) = (В > 25),
(В < 27) + (В < 25) = (В < 27).
Условия В > 25 и В < 27 одновременно выполняются только для целого числа В = 26.
Следующая страница 
Вопросы и задания, Задачи
Cкачать материалы урока
