Уроки 84 - 86
Рекурсия
§61. Рекурсия
Содержание урока
Как работает рекурсия
Как работает рекурсия
Рассмотрим вычисление факториала N!: так называют произведение всех натуральных чисел от 1 до заданного числа N! = 1 • 2 • 3 • ... • N. Факториал может быть также введён с помощью рекуррентной формулы, которая связывает факториал данного числа с факториалом предыдущего 1:
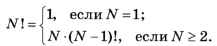
1 В математике принято, что факториал нуля равен 1. Поэтому равенство 0! = 1 можно тоже принять за базовый случай
Здесь первая часть описывает базовый случай (условие окончания рекурсии), а вторая — переход к следующему шагу. Запишем соответствующую функцию на школьном алгоритмическом языке, добавив в начале и в конце операторы вывода:
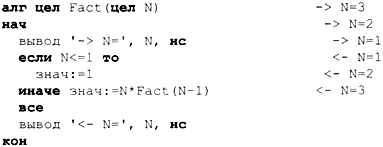
Справа от программы показан протокол её работы при вызове Fact(3) (для наглядности сделаны отступы, показывающие вложенность вызовов). Из протокола видно, что вызов Fact (2) происходит раньше, чем заканчивается вызов Fact(3). Это значит, что компьютеру нужно где-то (без помощи программиста) запомнить состояние программы (в том числе значения всех локальных переменных) и адрес, по которому нужно вернуться после завершения вызова Fact (2) . Для этой цели используется стек.
Стек (англ, stack — кипа, стопка) — особая область памяти, в которой хранятся локальные переменные и адреса возврата из процедур и функций.
Один из регистров процессора называется указателем стека (англ, stack pointer, SP) — в нём записан адрес последней занятой ячейки стека. При вызове процедуры в стек помещаются значения всех её параметров, адрес возврата и выделяется место под локальные переменные.
На рисунке 8.4, а показано начальное состояние стека, серым цветом выделены занятые ячейки. Когда функция Fact вызывается из основной программы с параметром 3, в стек записывается значение параметра, затем — адрес возврата А, и выделяется место для локальной переменной знач, в которую будет записан результат 2 (рис. 8.4, б). При втором и третьем вложенных вызовах в стек добавляются аналогичные блоки данных (рис. 8.4, в и г). Заметьте, что в нашем случае адрес возврата AF (точка внутри функции Fact после рекурсивного вызова) в последних двух блоках будет один и тот же.
2 Результат функции, как правило, передается в вызывающую программу через регистры, но во время работы функции хранится в стеке.
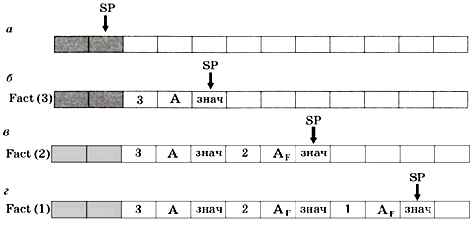
Рис. 8.4
Когда выполняется возврат из процедуры, состояние стека изменяется в обратную сторону: г — в — б — а.
Что же следует из этой схемы? Во-первых, с каждым новым вызовом расходуется дополнительная стековая память. Если вложенных вызовов будет очень много (или если процедура создаёт много локальных переменных), эта память закончится, и программа завершится аварийно.
Во-вторых, при каждом вызове процедуры некоторое время затрачивается на выполнение служебных операций (занесение данных в стек и т. п.), поэтому, как правило, рекурсивные программы выполняются несколько дольше, чем аналогичные нерекурсивные.
Всегда ли можно написать нерекурсивную программу? Оказывается, всегда. Доказано, что любой рекурсивный алгоритм может быть записан без использования рекурсии. Хотя:
• часто при этом программа усложняется и становится менее понятной;
• нерекурсивная версия нередко требует дополнительного расхода памяти.
Например, для вычисления факториала можно использовать обычный цикл:
В данном случае такой итерационный (т. е. повторяющийся, циклический) алгоритм значительно лучше, чем рекурсивный: он не расходует стековую память и выполняется быстрее. Поэтому здесь нет никакой необходимости использовать рекурсию.
Итак, рекурсия — это мощный инструмент, заменяющий циклы в задачах, которые можно свести к более простым задачам того же типа. В сложных случаях использование рекурсии позволяет значительно упростить программу, сократить её текст и сделать более понятной.
Вместе с тем, если существует простое решение задачи без использования рекурсии, лучше применить именно его. Нужно стараться обходиться без рекурсии, если вложенность вызовов получается очень большой или подпрограмма использует много локальных данных.
Следующая страница 
Вопросы и задания
Cкачать материалы урока
