Урок 7
Восьмеричная и шестнадцатеричная системы счисления
§12. Восьмеричная система счисления. §13. Шестнадцатеричная система счисления

Содержание урока

§12. Восьмеричная система счисления

Восьмеричная система

Алгоритм перевода восьмеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

Вопросы и задания

Задачи

§13. Шестнадцатеричная система счисления

§12. Восьмеричная система счисления

Алгоритм перевода восьмеричного числа в двоичную систему счисления

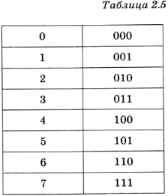
1. Перевести значение каждой цифры (отдельно) в двоичную систему. Записать результат в виде триады, добавив, если нужно, нули в начало (табл. 2.5).

2. Соединить триады в одно «длинное» двоичное число.

Например: 35721₈ = 11 101 111 010 001₂. В этой записи триады специально отделены друг от друга пробелом. Обратите внимание, что все триады дополнены слева нулями до трёх цифр:

2 = 10₂ = 010₂,

1 = 1₂ = 001₂.

Для самой первой триады это делать необязательно, потому что лидирующие нули в записи числа никак его не меняют. Напротив, если «потерять» нули в середине числа, получится неверный результат.

Следующая страница Алгоритм перевода двоичного числа в восьмеричную систему счисления

Cкачать материалы урока