Урок 7
Восьмеричная и шестнадцатеричная системы счисления
§12. Восьмеричная система счисления. §13. Шестнадцатеричная система счисления
Содержание урока
§12. Восьмеричная система счисления
Алгоритм перевода восьмеричного числа в двоичную систему счисления
Алгоритм перевода двоичного числа в восьмеричную систему счисления
§13. Шестнадцатеричная система счисления
§12. Восьмеричная система счисления
Алгоритм перевода двоичного числа в восьмеричную систему счисления
1. Разбить двоичное число на триады, начиная справа. В начало самой первой триады добавить слева нули, если это необходимо.
2. Перевести каждую триаду (отдельно) в восьмеричную1 систему счисления.
1 Заметим, что значение цифры в восьмеричной системе счисления совпадает со значением этой же цифры в десятичной системе.
3. Соединить полученные цифры в одно «длинное» число.
Например, переведём в восьмеричную систему число 10100111001011101112. Разобьём его на триады (начиная справа), в начало числа нужно добавить два нуля (они подчёркнуты): 10100111001011101112 = 001 010011 100 101 110 1112.
Далее по табл. 2.5 переводим каждую триаду в восьмеричную систему: 10100111001011101112 = 12345678.
Теперь представьте себе объём вычислений, который потребуется для решения этой задачи через десятичную систему.
При вычислениях в восьмеричной системе нужно помнить, что максимальная цифра — это 7. Перенос при сложении возникает тогда, когда сумма в очередном разряде получается больше 7. Заём из старшего разряда равен 108 = 8, а все «промежуточные» разряды заполняются цифрой 7 — старшей цифрой системы счисления. Приведём примеры сложения и вычитания:
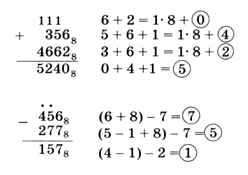
В примере на сложение запись 1 • 8 + 2 означает, что получилась сумма, большая 7, которая не помещается в один разряд. Единица идёт в перенос, а двойка остаётся в этом разряде. В записи операций при выполнении вычитания запись «-1» означает, что из этого разряда раньше был заём (его значение уменьшилось на 1), а запись «+8» означает заём из старшего разряда.
С помощью восьмеричной системы удобно кратко записывать содержимое областей памяти, содержащих количество битов, кратное трём. Например, 6-битные данные «упаковываются» в две восьмеричные цифры. Некоторые компьютеры 1960-х годов использовали 24-битные и 36-битные данные, они записывались соответственно с помощью 8 и 12 восьмеричных цифр. Восьмеричная система использовалась даже для компьютеров с 8-битной ячейкой памяти (PDP-11, ДВК), но позднее была почти вытеснена шестнадцатеричной системой (см. далее).
Сейчас восьмеричная система применяется, например, для установки прав на доступ к файлу в операционной системе Linux (и других Unix-системах) с помощью команды chmod. Режим доступа кодируется тремя битами, которые разрешают чтение (r, read, старший бит), запись (w, write) и выполнение файла (х, execute, младший бит). Код 7 = 1112 (rwx) означает, что все биты установлены (полный доступ), а код 5 = 1012 (r-х) разрешает чтение и выполнение файла, но запрещает его изменение.
Следующая страница  Вопросы и задания
Вопросы и задания

