Урок 10
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы

Содержание урока

§18. Логика и компьютер

§19. Логические операции

§20. Диаграммы

Диаграммы Венна или круги Эйлера

Задачи

§20. Диаграммы

Диаграммы Венна или круги Эйлера

Выражения, зависящие от небольшого количества переменных (обычно не более четырёх), удобно изображать в виде диаграмм, которые называют диаграммами Венна или кругами Эйлера.

На такой диаграмме каждой переменной соответствует круг, внутри которого она равна единице, а вне его — нулю. Круги могут пересекаться. Области, в которых рассматриваемое логическое выражение истинно, закрашиваются каким-либо цветом. На рисунке 3.14 приведены диаграммы для простейших операций с одной и двумя переменными. Серым цветом залиты области, где рассматриваемое выражение равно единице.

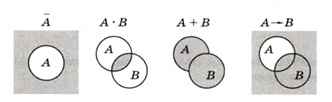
Рис. 3.14

Такие диаграммы часто используются при работе с множествами: операция «И» соответствует пересечению двух множеств, а «ИЛИ» — объединению.

Для трёх переменных диаграмма будет немного сложнее. Для каждой из областей показанной на рис. 3.15 диаграммы запишем логические выражения.

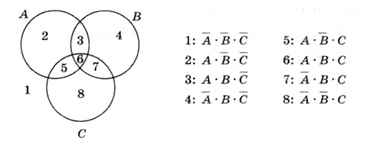
Рис. 3.15

Для того чтобы найти выражение для объединения двух или нескольких областей, надо применить логическое сложение (операцию «ИЛИ») к выражениям для всех составляющих. Например, выражение для объединения областей 3 и 4 имеет вид

3 + 4 : А • В • С + А • В • С.

Вместе с тем если не обращать внимания на область А, то можно заметить, что справедлива формула

3 + 4 : В • С..

Это означает, что логические выражения в некоторых случаях можно упростить. Как это делается, вы узнаете в следующем параграфе.

Диаграммы удобно применять для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы в ответ на какой-то запрос. Рассмотрим следующую задачу.

Следующая страница Задачи

Cкачать материалы урока