Уроки 5 - 7
Измерение информации (§§ 3 - 4)

Содержание урока

Измерение информации. Алфавитный подход

Измерение информации. Содержательный подход

Неопределенность знания и количество информации

«Главная формула» информатики

Формула Хартли

Вопросы и задания

Практическая работа № 1.2 "Измерение информации"

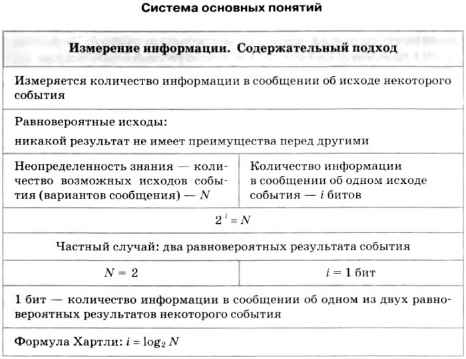
Измерение информации. Содержательный подход

Формула Хартли

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения

2ⁱ = 3.

будет дробным числом, лежащим между 1 и 2, поскольку 2¹ = 2 < 3, а 2² = 4 > 3. А как точнее узнать это число?

В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:

i = log₂ N.

Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от А — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:

log₂ 2 = 1, log₂ 4 = 2, log₂ 8 = 3.

Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

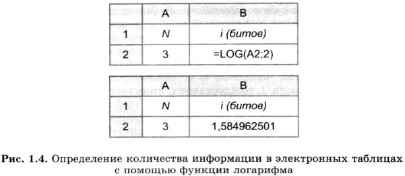
В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой: i = log₂3 = 1,584962501 (бита).

Формула для измерения количества информации: i = log₂N была предложена американским ученым Ральфом Хартли — одним из основоположников теории информации.

Формула Хартли: i = log₂ N
Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.

Следующая страница Вопросы и задания