Уроки 8 - 9
Представление чисел в компьютере (§ 5)

Содержание урока

Введение

Представление чисел

Целые числа в компьютере

Вещественные числа в компьютере

Практическая работа № 1.3 "Представление чисел"

Целые числа в компьютере

Правило № 4: в памяти компьютера числа хранятся в двоичной системе счисления*. С двоичной системой счисления вы знакомы из курса информатики 7-9 классов. Например, если под целое число выделяется ячейка памяти размером в 16 битов, то самое большое целое положительное число будет таким:

В десятичной системе счисления оно равно:

2¹⁵ - 1 = 32 767.

---

* Конечно, и «внутри калькулятора» числа представляются в двоичном виде. Однако мы в это вдаваться не будем, рассмотрев лишь внешнее представление. Пример с калькулятором нам нужен был только для иллюстрации проблемы ограниченности.

Здесь первый бит играет роль знака числа. Ноль — признак положительного числа. Самое большое по модулю отрицательное число равно -32 768. Напомним (это было в курсе информатики основной школы), как получить его внутреннее представление:

1) перевести число 32 768 в двоичную систему счисления; это легко, поскольку 32 768 = 2¹⁵:

1000000000000000;

2) инвертировать этот двоичный код, т. е. заменить нули на единицы, а единицы — на нули:

0111111111111111;

3) прибавить единицу к этому двоичному числу (складывать надо по правилам двоичной арифметики), в результате получим:

Единица в первом бите обозначает знак «минус». Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.

Если под целое число в памяти компьютера отводится N битов, то диапазон значений целых чисел:

[-2^N-1, 2^N~1 - 1],

т. е. ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Отсюда же следует и конечность множества целых чисел.

Мы рассмотрели формат представления целых чисел со знаком, т. е. положительных и отрицательных. Бывает, что нужно работать только с положительными целыми числами. В таком случае используется формат представления целых чисел без знака. В этом формате самое маленькое число — ноль (все биты — нули), а самое большое число для 16-разрядной ячейки:

В десятичной системе это 2¹⁶ - 1 = 65 535, примерно в два раза больше по модулю, чем в представлении со знаком.

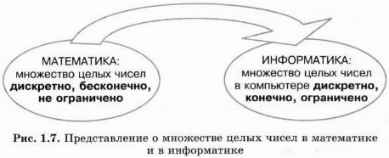
Из всего сказанного делаем вывод: целые числа в памяти компьютера — это дискретное, ограниченное и конечное множество.

Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака. Шаг в компьютерном представлении последовательности целых чисел, как и в математическом, остается равным единице.

Рисунок 1.7 отражает то обстоятельство, что при переходе от математического представления множества целых чисел к представлению, используемому в информатике (компьютере), происходит переход к ограниченности и конечности.

Следующая страница Вещественные числа в компьютере