Уроки 8 - 9
Представление чисел в компьютере (§ 5)
Содержание урока
Вещественные числа в компьютере
Практическая работа № 1.3 "Представление чисел"
Вещественные числа в компьютере
Понятие вещественного (действительного) числа в математику ввел Исаак Ньютон в XVIII веке. В математике множество вещественных чисел непрерывно, бесконечно и не ограничено. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел, что и означает непрерывность множества.
Как мы говорили выше, числа в компьютере (в том числе и вещественные) представлены в двоичной системе счисления. Покажем, что множество вещественных чисел в компьютере дискретно, ограничено и конечно. Нетрудно догадаться, что это, так же как и в случае целых чисел, вытекает из ограничения размера ячейки памяти.
Снова для примера возьмем калькулятор с десятиразрядным индикаторным табло. Экспериментально докажем дискретность представления вещественных чисел. Выполним на калькуляторе деление 1 на 3. Из математики вам известно, что 1/3 — это рациональная дробь, представление которой в виде десятичной дроби содержит бесконечное количество цифр: 0,3333333333... (3 в периоде). На табло калькулятора вы увидите:

Первый разряд зарезервирован под знак числа. После запятой сохраняется 8 цифр, а остальные не вмещаются в разрядную сетку (так это обычно называют). Значит, это не точное значение, равное 1/3, а его «урезанное» значение.
Следующее по величине число, которое помещается в разрядную сетку:

Оно больше предыдущего на 0,00000001. Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:

Оно тоже отделено от своего «соседа справа» по числовой оси шагом 0,00000001. Отсюда делаем вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, поскольку числа отделены друг от друга конечными отрезками.
А теперь выясним вот что: будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел)?
Вычислим выражение 100000/3. Получим:

Это число в 100 000 раз больше предыдущего и, очевидно, тоже приближенное. Легко понять, что следующее вещественное число, которое можно получить на табло калькулятора, будет больше данного на 0,0001. Шаг стал гораздо больше.
Отсюда приходим к выводу: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.
Если отметить на числовой оси точные значения вещественных чисел, которые представимы в калькуляторе, то эти точки будут расположены вдоль оси неравномерно. Ближе к нулю — гуще, дальше от нуля — реже (рис. 1.8).

Все выводы, которые мы делаем на примере калькулятора, полностью переносятся на компьютер с переходом к двоичной системе счисления и с учетом размера ячейки компьютера, отводимой под вещественные числа. Неравномерное расположение вещественных чисел, представимых в компьютере, также имеет место.
Ответим на вопрос: ограничено ли множество вещественных чисел в памяти компьютера? Если продолжать эксперименты с калькулятором, то ответ на этот вопрос будет таким: да, множество вещественных чисел в калькуляторе ограничено.
Причиной тому служит все та же ограниченность разрядной сетки. Отсюда же следует и конечность множества.
Самое большое число у разных калькуляторов может оказаться разным. У самого простого это будет то же число, что мы получали раньше: 999999999. Если прибавить к нему единицу, то калькулятор выдаст сообщение об ошибке. А на другом, более «умном» и дорогом, калькуляторе прибавление единицы приведет к такому результату:

Данную запись на табло надо понимать так: 1 • 109.
Такой формат записи числа называется форматом с плавающей запятой, в отличие от всех предыдущих примеров, где рассматривалось представление чисел в формате с фиксированной запятой.
Число, стоящее перед буквой «е», называется мантиссой, а стоящее после — порядком. «Умный калькулятор» перешел к представлению чисел в формате с плавающей запятой после того, как под формат с фиксированной запятой не стало хватать места на табло.
В компьютере то же самое: числа могут представляться как в формате с фиксированной запятой (обычно это целые числа), так и в формате с плавающей запятой.
Но и для форматы с плавающей запятой тоже есть максимальное число. В нашем «подопытном» калькуляторе это число:

То есть 99999 • 1099. Самое большое по модулю отрицательное значение -99999 • 1099. Данные числа являются целыми, но именно они ограничивают представление любых чисел (целых и вещественных) в калькуляторе.
В компьютере все организовано аналогично, но предельные значения еще больше. Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.
Рассмотрим пример: пусть под все число в компьютере выделяется 8 байтов — 64 бита, из них под порядок — 2 байта, под мантиссу — 6 байтов. Тогда диапазон вещественных чисел, в переводе в десятичную систему счисления, оказывается следующим:
±(5 • 10-324 - 1,7 • 10308).
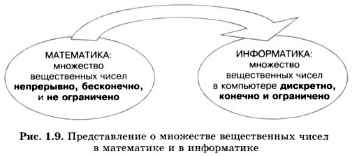
Завершая тему, посмотрим на рис. 1.9. Смысл, заложенный в нем, такой: непрерывное, бесконечное и не ограниченное множество вещественных чисел, которое рассматривает математика, при его представлении в компьютере обращается в дискретное, конечное и ограниченное множество.

Вопросы и задания
1. Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
2. Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.
3. Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.
4. Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.
5. Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
6. На какие две части делится число в формате с плавающей запятой?
Следующая страница  Практическая работа № 1.3 "Представление чисел"
Практическая работа № 1.3 "Представление чисел"

