Уроки 23 - 25
Логические величины и выражения, программирование ветвлений
Практикум
Практическая работа № 3.2
"Программирование логических выражений"
Практическая работа № 3.3
"Программирование ветвящихся алгоритмов"

Содержание урока

Логические величины, операции, выражения

Программирование ветвлений

Пример поэтапной разработки программы решения задачи

Работа 3.2. Программирование логических выражений

Работа 3.3. Программирование ветвящихся алгоритмов

Логические величины, операции, выражения

С элементами математической логики вы уже встречались в курсе информатики основной школы, изучая способы записи запросов к базе данных и условной функции ЕСЛИ в электронных таблицах, основы алгоритмизации и программирования. Повторим основные понятия логики с целью дальнейшего углубления ваших знаний в использовании ее для программирования.

К числу основных понятий логики относятся: высказывание, логическая величина, логические операции, логические выражения и формулы.

Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывании можно сказать, истинно оно или ложно.

Например, высказывание «На улице идет дождь» будет истинным или ложным в зависимости от состояния погоды в данный момент. Истинность высказывания «Значение А больше, чем В», записанного в форме неравенства: А > В, будет зависеть от значений переменных А и В.

Логические величины — понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается через логические величины.

Логическая константа: ИСТИНА или ЛОЖЬ.

Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, Y и др. — переменные логические величины, то, значит, они могут принимать значения только ИСТИНА или ЛОЖЬ.

Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок).

Логические операции

Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или ∧. Конъюнкция — двухместная операция; записывается в виде: А & В. Значением такого выражения будет ЛОЖЬ, если значение хотя бы одного из операндов ложно.

Дизъюнкция (логическое сложение). В русском языке этой связке соответствует союз ИЛИ. В математической логике она обозначается знаком v. Дизъюнкция — двухместная операция; записывается в виде: A v В. Значением такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.

Отрицание. В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что ...»). Отрицание — унарная (одноместная) операция; записывается в виде: ¬ А или Ā.

Правила выполнения рассмотренных логических операций отражены в следующей таблице, которая называется таблицей истинности логических операций (здесь И означает «истина», Л — «ложь»):

Логическая формула — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.

Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок выполнения операций влияют скобки, которые можно использовать в логических формулах.

Например: (А & В) v (¬ А & В) v (¬ А & ¬ В).

Пример. Вычислить значение логической формулы:

¬ X & Y v X & Z,

если логические переменные имеют следующие значения: X = ЛОЖЬ, Y = ИСТИНА, Z = ИСТИНА.

Решение. Отметим цифрами сверху порядок выполнения операций в формуле:

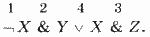
Используя таблицу истинности, вычислим формулу по шагам:

1)	 ЛОЖЬ = ИСТИНА;
2)	 ИСТИНА & ИСТИНА = ИСТИНА;
3)	 ЛОЖЬ & ИСТИНА = ЛОЖЬ;
4)	 ИСТИНА v ЛОЖЬ = ИСТИНА.
Ответ: ИСТИНА.

Логические функции на области числовых значений

Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значения числовой переменной X множеству положительных чисел выражается через высказывание: «X больше нуля». Символически это записывается так: Х > 0. В алгебре такое выражение называют неравенством. В логике — отношением.

Отношение X > 0 может быть истинным или ложным. Если X — положительная величина, то оно истинно, если отрицательная, то ложно. В общем виде отношение имеет следующую структуру:

< выражение 1 > < знак отношения > < выражение 2 >

Здесь выражения 1 и 2 — некоторые математические выражения, принимающие числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. Знаки отношений могут быть следующими:

Итак, отношение — это простое высказывание, а значит, логическая величина. Оно может быть как постоянной: 5 > 0 — всегда ИСТИНА, 3 * 6 : 2 — всегда ЛОЖЬ; так и переменной: а < b, х + 1 = с - d. Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.

Отношение можно рассматривать как логическую функцию от числовых аргументов. Например: F(x) = (х > 0) или Р(х, у) = = (х < у). Аргументы определены на бесконечном множестве действительных чисел, а значения функции — на множестве, состоящем из двух логических величин: ИСТИНА, ЛОЖЬ.

Логические функции от числовых аргументов еще называют термином предикат. В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.

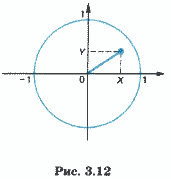
Пример 1. Записать предикат (логическую функцию) от двух вещественных аргументов X и Y, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и Y лежит внутри единичной окружности с центром в начале координат (рис. 3.12).

Из геометрических соображений понятно, что для всех точек, лежащих внутри единичной окружности, будет истинным значение следующей логической функции:

F(Х, У) = (X² + У² < 1).

Для значений координат точек, лежащих на окружности и вне ее, значение функции F будет ложным.

Пример 2. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри кольца с центром в начале координат, и радиусами R1 и R2.

Поскольку значения R1 и R2 — переменные величины, искомая логическая функция будет иметь четыре аргумента: X, У, R1, R2. Возможны две ситуации:

1) R1² < X² + У² < R2² и R1 < R2: R1 — внутренний радиус, R2 — внешний радиус;

2) R2² < X² + У² < R1² и R2 < R1: R2 — внутренний радиус, R1 — внешний радиус.

Объединив дизъюнкцией оба этих утверждения и записав их по правилам алгебры логики, получим следующую логическую функцию:

F(Х, У, R1, R2) = (((X² + У²) > R1²) & ((X² + У²) < R2²) & R1 < R2) v (((X² + У²) > R2²) & ((X² + У²) < R1²) & R2 < R1).

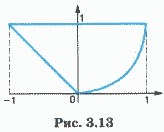
Пример 3. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри фигуры, ограниченной жирными линиями на рис. 3.13.

Фигура ограничена тремя границами, описываемыми уравнениями:

У = -X — левая граница, линейная функция;

У = 1 — верхняя граница, константа;

У = X² — правая граница, парабола.

Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами:

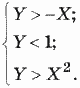
Во внутренних точках все эти три отношения являются одно-временно истинными. Поэтому искомый предикат имеет вид:

F(X, У) = (У > -X) & (Y < 1) & (У > X²).

Логические выражения на Паскале

Уже говорилось о том, что в Паскале имеется логический тип данных.

Логические константы: true (истина), false (ложь).

Логические переменные: описываются с типом Boolean.

Операции отношения: осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними. Знаки операций отношения: = (равно), <> (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно).

Логические операции: not — отрицание, and — логическое умножение (конъюнкция), or — логическое сложение (дизъюнкция), хоr — исключающее ИЛИ. Таблица истинности для этих операций (Т — true; F — false):

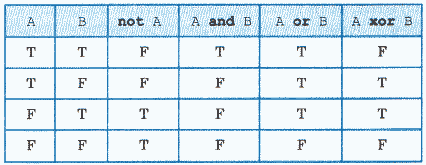
Логическое выражение может состоять из логических констант и переменных, отношений, логических операций. Логическое выражение принимает значение true или false.

Например, логическая формула ¬ X & У v X & Z на Паскале запишется в виде следующего логического выражения:

not X and Y or X and Z,

где X, Y, Z — переменные типа Boolean.

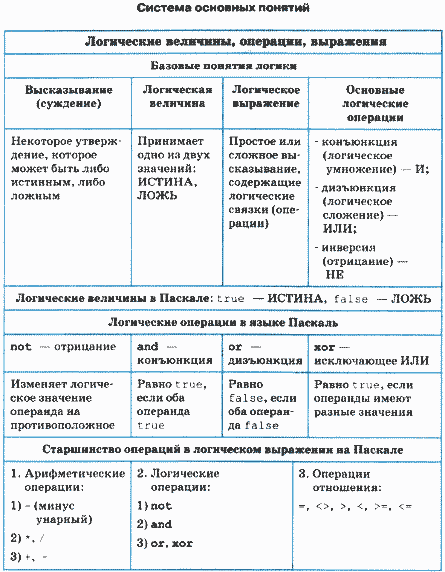
Логические операции располагаются в следующем порядке по убыванию старшинства (приоритета): 1) not, 2) and, 3) or, xor. Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 ≤ X ≤ 50 соответствует следующее логическое выражение:

(1 <= Х) and (Х <= 50)

Логическая функция odd(x) принимает значение true, если значение целочисленного аргумента х является нечетным, иначе — false.

Для правильной записи сложного логического выражения (предиката) нужно учитывать относительные приоритеты арифмети-ческих, логических операций и операций отношений, поскольку все они могут присутствовать в логическом выражении. По убыванию приоритета операции располагаются в следующем порядке.

1.	 Арифметические операции:
- (минус унарный)
*, /
+, -
2.	 Логические операции:
not
and
or, xor
3.	 Операции отношения:
=, <>, >, <, >=, <=

Еще раз обратите внимание, что в логическом выражении, соответствующем предикату из примера 3:

(Y > -X) and (Y < 1) and (Y > X * X),

операции отношения заключены в скобки, поскольку они младше логических операций, а выполняться должны раньше.

Вопросы и задания

1. Какого типа величина получается при вычислении отношения (неравенства) между числами?

2. Что такое предикат? Приведите примеры.

3. Запишите на языке алгебры логики логические функции, которые будут принимать значение ИСТИНА, если справедливы следующие утверждения, и ЛОЖЬ — в противном случае:

а) все числа X, Y, Z равны между собой;
б) из чисел X, Y, Z только два равны между собой;
в) каждое из чисел X, Y, Z положительно;
г) только одно из чисел X, У, Z положительно;
д) значения чисел X, У, Z упорядочены по возрастанию.

4. Все формулы, полученные при решении предыдущей задачи, запишите в виде логических выражений на Паскале.

5. Постройте таблицу истинности для логической формулы:

¬X & Y v X & Z.

Пояснение: в таблице истинности должны быть вычислены значения формулы для всех вариантов значений логических переменных: X, У, Z. Следовательно, таблица будет содержать 2³ = 8 строк и 4 столбца: значения X, У, Z и результат. В таблицу можно добавить дополнительные столбцы, содержащие результаты промежуточных операций.

6. Вычислите значения следующих логических выражений, записанных на Паскале:

Пояснения: odd(x) — логическая функция определения четности аргумента, равна true, если х — нечетное, и равна false, если х — четное; trunc (х) — целочисленная функция от вещественного аргумента, возвращающая ближайшее целое число, не превышающее х по модулю.

Следующая страница Программирование ветвлений