Уроки 23 - 25
Логические величины и выражения, программирование ветвлений
Практикум
Практическая работа № 3.2
"Программирование логических выражений"
Практическая работа № 3.3
"Программирование ветвящихся алгоритмов"

Содержание урока

Логические величины, операции, выражения

Программирование ветвлений

Пример поэтапной разработки программы решения задачи

Работа 3.2. Программирование логических выражений

Работа 3.3. Программирование ветвящихся алгоритмов

Пример поэтапной разработки программы решения задачи

Постановка задачи и формализация

Словом «задача» называют проблему, которая требует решения. Решение задачи начинается с ее постановки. На этапе постановки задачи в терминах предметной области (физики, экономики, биологии и др.) определяются исходные данные и результаты, которые надо получить.

Следующий этап — формализация задачи. Чаще всего процесс формализации означает перевод задачи на язык математики: формул, уравнений, неравенств, систем уравнений, систем неравенств и т. п.

Подробнее о формализации будет рассказано в разделе, посвященном информационному моделированию (в 11 классе). Некоторые представления об этом вы уже имеете из курса информатики для 7-9 классов.

Решение полученной математической задачи требует знания математики, умения выполнять анализ математической задачи. Такой анализ необходим для того, чтобы построить правильный алгоритм решения, обладающий всеми свойствами алгоритма.

Анализ математической задачи

Пусть в результате формализации некоторой задачи было получено квадратное уравнение: ах² + bх + с = 0, где коэффициенты а, b, с являются исходными данными. Требуется решить это уравнение, т. е. найти его корни. Проведем анализ этой математической задачи.

Рассмотрим различные варианты значений исходных данных, которые приводят к разным результатам для решающего ее алгоритма. Ограничимся только поиском вещественных корней уравнения.

Проанализируем все возможные варианты множества значений коэффициентов а, b, с:

Построение алгоритма

Построим блок-схему алгоритма решения квадратного уравнения (рис. 3.15), учитывающего все ситуации, описанные в анализе задачи. Здесь вместо слов «да» и «нет» использованы знаки « + » и « — ».

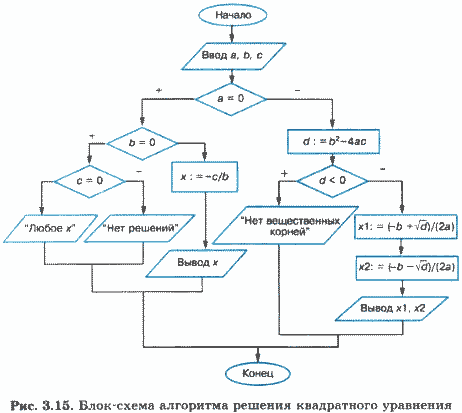
Построенный алгоритм, несомненно, удовлетворяет свойству универсальности по отношению к исходным данным. Запишем этот же алгоритм на учебном Алгоритмическом языке.

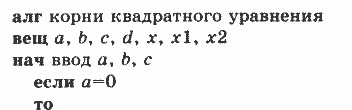
Обратите внимание на смещения строк в тексте алгоритма — соблюдается принцип структуризации внешнего вида ("Программирование линейных алгоритмов"). Повторим его: запись всякой вложенной структуры должна быть смещена на несколько позиций вправо относительно записи внешней структуры, а конструкции одного уровня вложенности записываются на одном вертикальном уровне.

Программирование

Алгоритмический язык (АЯ) — это язык описания алгоритмов с русскими служебными словами. После того как алгоритм записан на АЯ, составление программы на Паскале становится несложной задачей. Основное внимание следует уделять строгому соблюдению синтаксических правил языка. Правило смещения строк в тексте программы то же, что было сформулировано (в "Программирование линейных алгоритмов") для АЯ. Соответствующие друг другу служебные слова Begin и End должны располагаться друг под другом.

Чем больше текст программы, тем больше вероятность совершения ошибок при ее записи и вводе в компьютер. Ошибки, нарушающие правила грамматики языка, называются синтаксическими ошибками. Поиск и устранение синтаксических ошибок в программе называются отладкой. Отладить программу программисту помогает система программирования на данном языке, которая автоматически обнаруживает ошибки и сообщает о них программисту.

Тестирование программы

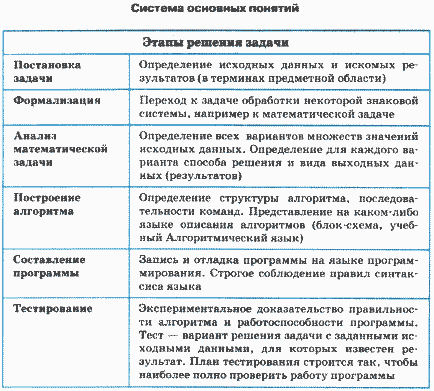
Тестирование — это этап, на котором экспериментально доказывается правильность алгоритма, заключенного в программе, и работоспособность программы. Тест — это вариант решения задачи с заданными исходными данными, для которых известен результат.

Предварительно должен быть составлен план тестирования. Для ветвящегося алгоритма должны быть протестированы все его ветви. В нашем примере пять ветвей, пять вариантов ответа. Значит, в плане тестирования должно быть не менее пяти вариантов теста.

В таблице 3.5 представлен план тестирования программы Roots и результаты проведенного тестирования.

Теперь, анализируя результаты тестирования, делаем вывод: правильность алгоритма и работоспособность программы доказаны.

Если какой-то из вариантов теста не дает ожидаемого результата, то в программе есть ошибки. Например, пусть программист ошибочно записал следующие операторы присваивания для вычисления корней:

Результаты всех тестов, кроме 4-го, совпали с ожидаемыми, а в 4-м тесте получилось: х1 = 4, х2 = -6. После этого программист обратит внимание на выражения для вычисления корней и исправит ошибки: либо заменит знак умножения на знак деления, либо заключит в скобки выражение 2*а.

Вопросы и задания

1. Сформулируйте основные цели этапов алгоритмического решения задачи.

2. Проанализируйте задачу решения биквадратного уравнения, составьте алгоритм и напишите программу на Паскале.

Следующая страница Работа 3.2. Программирование логических выражений