Уроки 23 - 25
Логические величины и выражения, программирование ветвлений
Практикум
Практическая работа № 3.2
"Программирование логических выражений"
Практическая работа № 3.3
"Программирование ветвящихся алгоритмов"

Содержание урока

Логические величины, операции, выражения

Программирование ветвлений

Пример поэтапной разработки программы решения задачи

Работа 3.2. Программирование логических выражений

Работа 3.3. Программирование ветвящихся алгоритмов

Работа 3.3. Программирование ветвящихся алгоритмов

Задание 1

Для каждой задачи составить программу с ветвящейся структурой, используя условный оператор IF.

Уровень 1

1. Даны два угла треугольника (в градусах). Определить, существует ли такой треугольник. Если да, то прямоугольный ли он.

2. На плоскости XOY задана своими координатами точка А. Указать, где она расположена: на какой оси или в какой координатной четверти.

3. Грузовой автомобиль выехал из одного города в другой со скоростью υ₁ км/ч. Через Ив этом же направлении выехал легковой автомобиль со скоростью υ₂ км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t₁ ч после своего выезда.

4. Написать программу нахождения суммы большего и меньшего из 3 чисел.

5. Написать программу, распознающую по длинам сторон среди всех треугольников прямоугольные. Если таковых нет, то вычислить величину угла С.

6. Найти max{min(a, b), min(c, d)}.

7. Составить программу, осуществляющую перевод величин из радианной меры в градусную или наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие.

Уровень 2

8. Заданы размеры А, В прямоугольного отверстия и размеры x, y, z кирпича. Определить, пройдет ли кирпич через отверстие.

9. Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат, заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это точки (х₁, у₁) и (х₂, 0), для второго — (х₃, у₃), (х₄, 0). Составить программу, определяющую, пересекаются ли данные прямоугольники, и вычисляющую площадь общей части, если они пересекаются.

10. В небоскребе N этажей и всего один подъезд; на каждом этаже по 3 квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры М. На какой этаж должен доставить лифт пассажира?

11. Написать программу, которая по заданным трем числам определяет, является ли сумма каких-либо двух из них положительной.

12. Известно, что из четырех чисел а₁, а₂, а₃ и а₄ одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.

13. Составить программу, которая проверяла бы, не приводит ли суммирование двух целых чисел А и В к переполнению (т. е. к результату большему, чем 32 767). Если будет переполнение, то сообщить об этом, иначе вывести сумму этих чисел.

Уровень 3

14. Заданы координаты (на плоскости) вершин четырехугольника. Определить, является ли он: а) ромбом; б) параллелограммом; в) прямоугольником; г) квадратом.

15. Для двух треугольных пирамид, заданных ребрами, определить, площадь полной поверхности которой из них больше и на сколько.

16. Дана точка А(х, у). Определить, принадлежит ли она треугольнику с вершинами в точках (х₁, у₁), (х₂, y₂), (х₃, у₃).

17. Написать программу, определяющую, будут ли прямые А₁х + В₁у + C₁ = 0 и А₂Х + В₂у + С₂ = О перпендикулярны. Если нет, то найти угол между ними.

18. Заданы координаты вершин прямоугольника: (х₁, у₁), (х₂, у₂), (х₃, у₃), (х₄, у₄). Определить площадь части прямоугольника, расположенной в I координатной четверти.

19. Найти координаты точек пересечения прямой у = kx + b и окружности радиуса R с центром в начале координат. В каких координатных четвертях находятся точки пересечения? Если точек пересечения нет или прямая касается окружности, выдать соответствующее сообщение.

20. Дана точка А(х, у). Определить, принадлежит ли она прямоугольнику с вершинами в точках (x₁, у₁), (х₂, у₂), (х₃, у₃), (x₄, у4)

Задание 2
Задачи на определение принадлежности точки области

Для каждой задачи составить программу, содержащую ветвления и определяющую, принадлежит ли точка с координатами (X, Y) заштрихованной области.

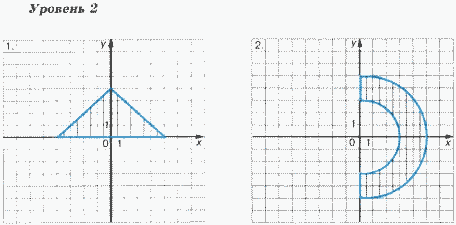
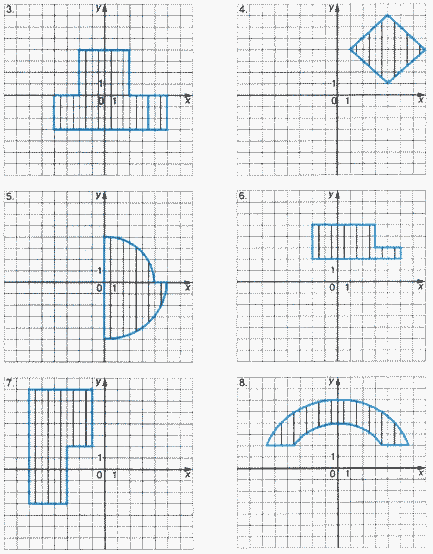
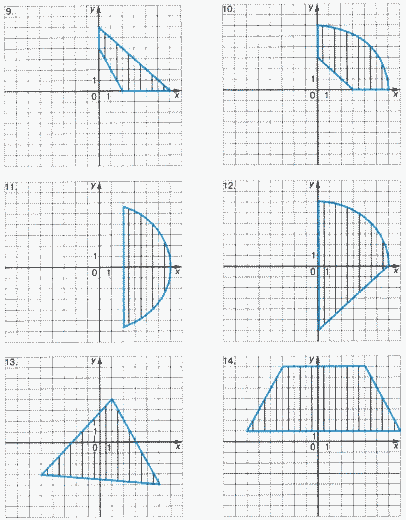
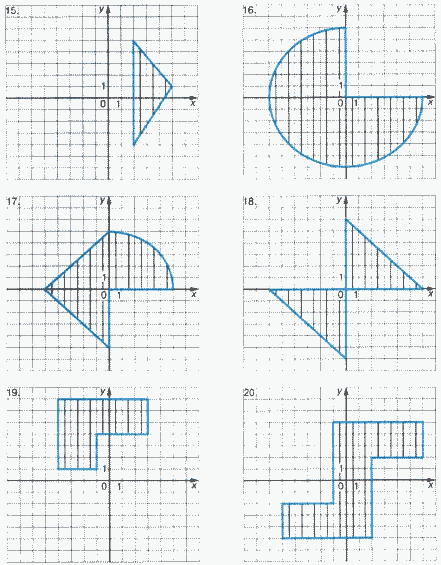
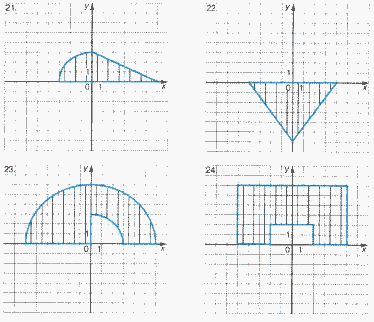
Задание 3
Задачи на использование оператора выбора

Для каждой задачи составить программу с ветвящейся структурой, используя оператор выбора SELECT CASE.

Уровень 1

1. Для каждой введенной цифры (0—9) вывести соответствующее ей название на английском языке (0 — zero, 1 — one, 2 — two, ...).

2. Составить программу, которая по данному числу (1-12) выводит название соответствующего ему месяца на английском языке.

3. Написать программу, которая по вводимому числу от 1 до 11 (номеру класса) выдает соответствующее сообщение «Привет, k-классник». Например, если k — 1, «Привет, первоклассник»; при k = 4: «Привет, четвероклассник».

4. Составить программу, позволяющую получить словесное описание школьных отметок (1 — плохо, 2 — неудовлетворительно, 3 — удовлетворительно, 4 — хорошо, 5 — отлично).

5. Написать программу, которая бы по введенному номеру единицы измерения (1 — дециметр, 2 — километр, 3 — метр, 4 — миллиметр, 5 — сантиметр) и длине отрезка L выдавала соответствующее значение длины отрезка в метрах.

6. Написать программу, которая бы по введенному номеру единицы измерения (1 — килограмм, 2 — миллиграмм, 3 — грамм, 4 — тонна, 5 — центнер) и массе М выдавала соответствующее значение массы в килограммах.

7. Даны два действительных положительных числа х и у. Арифметические действия над числами пронумерованы (1 — сложение, 2 — вычитание, 3 — умножение, 4 — деление). Составить программу, которая по введенному номеру выполняет то или иное действие над числами.

8. Написать программу, которая по номеру дня недели (целому числу от 1 до 7) выдает в качестве результата расписание уроков в вашем классе в этот день.

Уровень 2

9. Составить программу, которая по заданному году и номеру месяца определяет количество дней в этом месяце.

10. Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент) и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.

11. Пусть элементами прямоугольного равнобедренного треугольника являются: 1) катет а; 2) гипотенуза b; 3) высота, опущенная из вершины прямого угла на гипотенузу h; 4) площадь S. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника 12. В старояпонском календаре был принят 12-летний цикл. Годы внутри цикла носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. Написать программу, которая вводит номер некоторого года и печатает его название по старояпонскому календарю. (Справка: 1996 г. — год Крысы — начало очередного цикла.)

13. Для целого числа k от 1 до 99 напечатать фразу «Мне k лет», учитывая при этом, что при некоторых значениях k слово «лет» надо заменить на слово «год» или «года». Например, 11 лет, 22 года, 51 год.

14. Написать программу, которая по введенному числу от 1 до 12 (номеру месяца) выдает все приходящиеся на этот месяц праздничные дни (например, если введено число 1, то: 1 января — Новый год, 7 января — Рождество).

15. Дано натуральное число N. Если оно делится на 4, вывести на экран ответ N = 4k (где k — соответствующее частное); если остаток от деления на 4 равен 1, N = 4k + 1; если остаток от деления на 4 равен 2, N = 4k + 2; если остаток от деления на 4 равен 3, N = 4k + 3. Например, 12 = 4 • 3, 22 = 4 • 5 + 2.

16. Пусть элементами равностороннего треугольника являются: 1) сторона а; 2) площадь S; 3) высота h; 4) радиус вписанной окружности r; 5) радиус описанной окружности R. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.

Следующая страница Логические величины и выражения, программирование ветвлений