Уроки 30 - 31
Работа с массивами
Практикум
Практическая работа № 3.6
"Программирование обработки одномерных массивов"
Практическая работа № 3.7
"Программирование обработки двумерных массивов"

Содержание урока

Массивы

Типовые задачи обработки массивов

Работа 3.6. Программирование обработки одномерных массивов

Работа 3.7. Программирование обработки двумерных массивов

Типовые задачи обработки массивов

Заполнение массива

Значения массива могут задаваться вводом с клавиатуры, чтением из файла или вычислением в программе. В некоторых задачах статистического характера требуется заполнять массивы случайными числами.

Пример 1. Заполнить массив равномерно распределенными целыми случайными числами в диапазоне от 0 до 100.

Со стандартной функцией Random (х) вы уже знакомы. Напомним, что она возвращает псевдослучайное целое число в диапазоне от 0 до х - 1.

Если требуется изменить диапазон случайных чисел, то это всегда можно сделать путем сдвига. Например, если нужно получить числа в диапазоне от -50 до 50, то в программе пишется оператор присваивания:

X[i]:=Random(100)-50;

Для получения вещественных случайных чисел используется функция Random без аргумента. Она возвращает случайные дробные значения в диапазоне [0,1). С помощью сдвига и множителя эти значения можно привести к любому диапазону. Например, следующее выражение будет вычислять случайное вещественное число в диапазоне значений от -5 до 5: 10 * Random-5.

Пример 2. Заполнить верхнетреугольную матрицу указанного вида и вывести ее на экран.

Пояснение: для элементов M[i, j] матрицы М, расположенных в верхнем треугольнике (включая диагональ), выполняется следующее соотношение между индексами: j ≤ i.

Пример 3. Выбор максимального элемента. В одномерном массиве X из примера 1 требуется определить наибольшее значение среди значений элементов и его порядковый номер (индекс).

Идея алгоритма решения этой задачи следующая: чтобы в переменной ХМах получить максимальное значение массива X, сначала в нее заносится первое значение массива Х[1]. Затем значение ХМах поочередно сравнивается с остальными элементами массива, и каждое значение, большее Хmах, присваивается этой переменной. Для получения номера максимального элемента массива в целочисленной переменной imax следует записывать в нее номер элемента массива X одновременно с занесением значения в Хmах. На Алгоритмическом языке это запишется так:

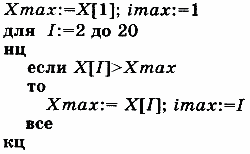
Заметим, что если в массиве X несколько значений, равных максимальному, то в imax будет получен первый номер из этих элементов. Чтобы получить номер последнего элемента, равного максимальному, нужно в ветвлении если заменить знак отношения > на >=. Для нахождение минимального элемента массива достаточно заменить знак отношения «больше» на «меньше».

Оформим в виде процедуры на Паскале подпрограмму поиска максимального элемента в одномерном массиве. Заполним одномерный массив случайными числами (как в примере 1). С помощью процедуры найдем в нем максимальное значение и индекс его первого вхождения в массив.

Процедура МахАггау имеет три параметра: исходный массив А, Мах А — переменную для найденного максимального значения, k — переменную для индекса максимального значения. При обращении к процедуре им соответствуют фактические параметры: X, Xmax, imax. Размер массива определяется глобальной константой n, значение которой используется как в основной программе, так и в процедуре.

Пример 4. Сортировка массива. В одномерном массиве X из N элементов требуется произвести перестановку значений так, чтобы они расположились по возрастанию, т. е. Х₁ ≤ Х₂ ≤ ... ≤ X_N.

Существует целый класс алгоритмов сортировки. Ниже описан алгоритм, который называется методом пузырька.

Идея алгоритма: производится последовательное упорядочивание смежных пар элементов массива: Х₁ и Х₂, Х₂ и Х₃,..., X_N-1 и X_N. В итоге максимальное значение переместится в X_N. Затем ту же процедуру повторяют до Х_N-1 и т. д., вплоть до цепочки из двух элементов Х₁ и Х₂. Такой алгоритм будет иметь структуру двух вложенных циклов, причем внутренний цикл переменной (сокращающейся) длины.

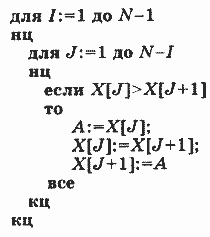
Для сортировки массива по убыванию значений достаточно заменить знак отношения «больше» на «меньше».

Запрограммируем на Паскале процедуру сортировки массива по возрастанию методом пузырька.

Пример 5. Ранее было рассмотрено описание двумерного массива, содержащего среднемесячные температуры за 10 лет, с 2001 по 2010 год. Определить, в каком году за этот период было самое теплое лето, т. е. в каком году была наибольшая средняя температура летних месяцев.

Идея решения: в одномерном массиве S получить средние температуры летних месяцев за каждый год из 10 лет. Затем найти номер наибольшего элемента в этом массиве, это и будет искомый год.

Вопросы и задания

1. Какими способами можно заполнить массив значениями?

2. Как можно вычислять целые случайные числа в диапазоне от -50 до 0?

3. Как можно вычислять вещественные случайные числа в диапазоне от 2,5 до 10?

4. Даны два вектора{х_i}, {y_i}, i = 1, ..., 10, упорядоченные по возрастанию. Соедините их в один вектор {z_i}, i = 1, ..., 20 так, чтобы сохранилась упорядоченность.

5. Дан массив, состоящий из 100 целых чисел. Выведите все числа, которые встречаются в этом массиве:

а) несколько раз;
б) только по одному разу.

6. В целочисленной матрице размером 10 х 10 найдите максимальное значение и индексы всех элементов, равных ему.

7. Матрицу размером 5 х 10 заполните случайными двоичными цифрами (0 и 1). Определите номер строки с наибольшим количеством нулей.

8. В двоичной матрице размером 10 х 10 (см. задание 7) найдите совпадающие строки.

Следующая страница Работа 3.6. Программирование обработки одномерных массивов