Уроки 30 - 31
Работа с массивами
Практикум
Практическая работа № 3.6
"Программирование обработки одномерных массивов"
Практическая работа № 3.7
"Программирование обработки двумерных массивов"

Содержание урока

Массивы

Типовые задачи обработки массивов

Работа 3.6. Программирование обработки одномерных массивов

Работа 3.7. Программирование обработки двумерных массивов

Работа 3.6. Программирование обработки одномерных массивов

Задание

Составить программу решения поставленной задачи по обработке одномерного массива (вектора). По возможности, использовать подпрограммы.

Уровень 1

1. Дана последовательность действительных чисел а₁, а₂, …, а_n. Выяснить, будет ли она возрастающей.

2. Дан массив из N действительных чисел. Подсчитать, сколько в нем отрицательных, положительных и нулевых элементов.

3. Даны действительные числа а₁, а₂, …, а_n. Поменять местами первый наибольший элемент с последним наименьшим элементом.

4. В заданном одномерном массиве поменять местами соседние элементы, стоящие на четных местах, с элементами, стоящими на нечетных местах.

5. Задана последовательность {X_i} из N вещественных чисел. Вычислить последовательность {S_i} по формуле:

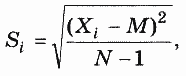
где М — среднее арифметическое значение последовательности X.

6. Задана последовательность из N целых чисел. Вычислить сумму тех элементов массива, порядковые номера которых совпадают со значением этого элемента.

7. Определить, сколько процентов от всего количества элементов последовательности целых чисел составляют нечетные элементы.

8. Дан массив Х_[N] целых чисел. Не используя других массивов, переставить его элементы в обратном порядке. 9. Задана последовательность из N вещественных чисел. Вычислить сумму чисел, порядковые номера которых являются простыми числами.

10. Последовательность а₁, а₂, …, а_2n состоит из нулей и единиц. Поместить в начало этой последовательности все нули, а затем все единицы.

11. Даны действительные числа а₁, а₂, …, а_2n. Найти:

mах(a₁ + а_2n, а₂ +а_2n-1, …, а_n + а_n+1).

12. Дана последовательность действительных чисел a₁ ≤ а₂ ≤ ... ≤ а_n. Вставить действительное число b в нее так, чтобы последовательность осталась неубывающей.

13. Дана последовательность целых чисел а₁, а₂, …, а_n. Указать пары чисел а_i, а_j, таких что a_i + а_j = m, где m - заданное целое число.

14. Даны координаты n (n ≤ 30) точек на плоскости: (Х₁, У₁), ..., (Х_п, Y_n). Найти номера пары точек, расстояние между которыми наибольшее (считать, что такая пара единственная).

15. Дан массив, состоящий из n натуральных чисел. Образовать новый массив, элементами которого будут элементы исходного, оканчивающиеся на цифру k.

16. Дан массив целых чисел. Найти в этом массиве минимальный элемент m и максимальный элемент М. Получить в порядке возрастания все целые числа из интервала (m; М), которые не входят в данный массив.

17. Даны две последовательности а₁, а₂, ..., а_n и b_х, b₂, ..., b_n (m < п). В каждой из них значения элементов различны. Верно ли, что все элементы второй последовательности входят в первую последовательность?

18. Вывести значения и номера наибольшего, наименьшего и наименее удаленного от среднего арифметического значения элементов данной последовательности вещественных чисел.

Уровень 3

19. Сформировать массив простых чисел, не больших заданного натурального числа N.

20. Сформировать массив простых множителей заданного числа.

21. В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные — в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.

22. В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х₁, у₁, х₂, у₂, х₃, у₃, и т. д. Определить:

а) минимальный радиус окружности с центром в начале координат, которая содержит все точки;
б) внутренний и внешний радиусы кольца с центром в начале координат, которое содержит все точки;
в) номера точек, которые могут являться вершинами квадрата;
г) номера точек, которые могут являться вершинами равнобедренного треугольника;
д) номера самых удаленных и наименее удаленных друг от друга точек;
е) три точки, которые являются вершинами треугольника, для которого разность точек вне его и внутри является минимальной.

23. Дана последовательность целых чисел. Найти количество различных чисел в этой последовательности.

24. На плоскости п точек заданы своими координатами, и также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью; множество всех треугольников, содержащихся внутри окружности.

25. Разделить массив на две части, поместив в первую элементы, большие среднего арифметического элементов массива, а во вторую — меньшие (части не сортировать).

26. Даны две последовательности а₁ < а₂ < ... < а_n и b₁ < b₂ < ... < b_m. Образовать из них новую последовательность чисел так, чтобы она тоже была неубывающей.

Примечание. Дополнительный массив не использовать.

27. Сортировка вставками. Дана последовательность чисел а₁, а₂, ..., а_n. Требуется переставить числа в порядке возрастания. Делается это следующим образом. Пусть а₁, а₂, ..., a_i — упорядоченная по неубыванию последовательность, т. е. а₁ < а₂ < ... < а_i. Берется следующее число a_i+1 и вставляется в последовательность так, чтобы новая последовательность была также возрастающей. Процесс производится до тех пор, пока все элементы от i+1 до n не будут перебраны.

Примечание. Место помещения очередного элемента в отсортированную часть найти с помощью двоичного поиска. Двоичный поиск оформить в виде отдельной функции.

28. Алгоритм сортировки фон Неймана. Упорядочить массив а₁, а₂, ..., а_n по неубыванию с помощью алгоритма сортировки слияниями:

1) каждая пара соседних элементов сливается в одну группу из двух элементов (последняя группа может состоять из одного элемента);

2) каждая пара соседних двухэлементных групп сливается в одну четырехэлементную группу и т. д.

При каждом слиянии новая укрупненная группа упорядочивается.

29. Шейкер-сортировка. Алгоритм «пузырьковой» сортировки легко улучшить. Разумно запомнить, производился ли на данном проходе какой-либо обмен. Если нет, то алгоритм можно закончить. Еще одно улучшение заключается в том, что периодически меняется направление сортировки, которое борется с некоторой асимметрией «пузырькового» метода. Написать программу, реализующую данный улучшенный алгоритм.

Следующая страница Работа 3.7. Программирование обработки двумерных массивов