Урок 12
§10. Представление чисел в позиционных системах счисления

10.3. Перевод чисел из g-ичной в десятичную систему счисления (продолжение)

Рассмотрим несколько примеров решения задач.

Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.

Запишем условие задачи иначе: 212_g = 57₁₀, q > 2. Представим в виде суммы разрядных слагаемых:

212_q = 2 • q² + 1 • q¹ + 2 • q⁰ =2q² + q + 2 = 57₁₀.

Решим уравнение: 2g² + q + 2 = 57.

2g² + q - 55 = 0.

Это квадратное уравнение, его корни х₁ = -5,5; х₂ = 5.

Так как основание системы счисления должно быть натуральным числом, то q — 5.

Пример 2. Все пятибуквенные слова, составленные из пяти букв А, И, Р, С, Т, записаны в алфавитном порядке.

Вот начало списка:

1. ААААА

2. ААААИ

3. ААААР

4. ААААС

5. ААААТ

6. АААИА

.....

Необходимо найти ответы на два вопроса.

1. На каком месте от начала списка стоит слово ИСТРА?

2. Сколько всего слов в этом списке?

Введём следующие обозначения: А — О, И — 1, Р — 2, С — 3, Т — 4. Перепишем в новых обозначениях исходный список:

1. 00000

2. 00001

3. 00002

4. 00003

5. 00004

6. 00010

.....

Теперь перед нами последовательность чисел от 0 до 44444, записанных в пятеричной системе счисления. При этом на 1-м месте в этой последовательности находится 0, на 2-м месте — 1, на 3-м месте — 2 и т. д. Это значит, что само число на единицу меньше того места (номера), которое оно занимает в последовательности.

Представив слово ИСТРА в новых обозначениях, получим 13420₅. Переведём это пятеричное число в десятичную систему счисления:

13420₅ = 1 • 5⁴ + 3 • 5³ + 4 • 5² + 2 • 5¹ + 0 • 5⁰ = 625 + 375 + 100 + 10 = 1110₁₀.

Это число находится в списке на 1111-м месте.

Чтобы выяснить, сколько всего слов в списке, запишем его самое последнее слово: ТТТТТ. Ему соответствует число 44444₅.

44444₅ = 4 • 5⁴ + 4 • 5³ + 4 • 5² + 4 • 5¹ + 4 • 5⁰ = 3124₁₀.

В списке это число стоит на 3125-м месте.

Вспомните о комбинаторике и предложите другой способ подсчёта количества слов в нашем списке.

Пример 3. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 60, запись которых в четверичной системе счисления оканчивается на 31.

В четверичной системе счисления используются цифры 0, 1, 2 и 3; число представляется в виде суммы разрядных слагаемых:

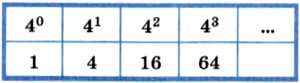
Из этой таблицы видно, что интересующие нас числа (≤ 60) не будут более чем трёхзначными. С учётом того что их запись заканчивается на 31, определим первую цифру (k):

k • 16 + 3 • 4 + 1 ≤ 60, k • 16 ≤ 47, k ∈ {0, 1, 2}.

Искомые числа: 31₄ = 13₁₀ (k = 0), 131₄ = 29₁₀ (k = 1), 231₄ = 45₁₀ (k = 2).

Cкачать материалы урока