Урок 27
§22. Логические задачи и способы их решения

22.3. Задачи на сопоставление. Табличный метод

Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов. От того, насколько удачно выбрана их структура, во многом зависит успешность решения задачи.

Пример 5. В летнем лагере в одной палатке жили Алёша, Боря, Витя и Гриша. Все они разного возраста, учатся в разных классах (с 7-го по 10-й) и занимаются в разных кружках: математическом, авиамодельном, шахматном и фотокружке. Выяснилось, что фотограф старше Гриши, Алёша старше Вити, а шахматист старше Алёши. В воскресенье Алёша с фотографом играли в теннис, а Гриша в то же время проиграл авиамоделисту в городки.

Определим, кто в каком кружке занимается.

В этой задаче речь идёт о высказывательной форме (предикате) вида «Ученик х занимается в кружке у». Требуется определить такие значения х и у, чтобы высказывательная форма превратилась в истинное высказывание.

Составим таблицу:

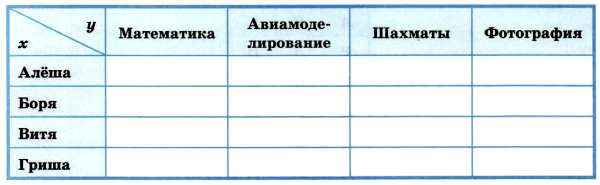
Рассмотрим условия:

1) фотограф старше Гриши;
2) Алёша старше Вити, а шахматист старше Алёши;
3) в воскресенье Алёша с фотографом играли в теннис, а Гриша в то же время проиграл авиамоделисту в городки.

Можем сделать выводы: Гриша — не фотограф (1); шахматист — не Алёша и не Витя (2); Алёша — не фотограф и не авиамоделист, Гриша — не фотограф и не авиамоделист (3). Отметим это в таблице:

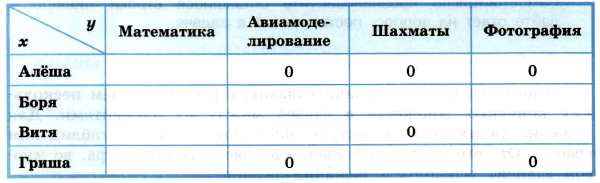
Имеющейся информации достаточно для того, чтобы утверждать, что Алёша занимается математикой, а Гриша — шахматами:

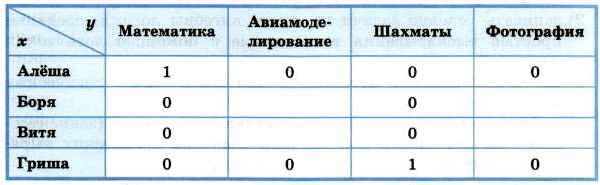
Из того, что Гриша — шахматист, и условий (1) и (2) следует, что мы можем расположить учеников по возрасту (в порядке возрастания): Витя — Алёша — шахматист Гриша — фотограф. Следовательно, Боря — фотограф. Этого достаточно, чтобы окончательно заполнить таблицу:

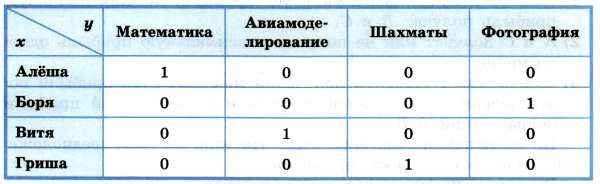
Итак, Алёша занимается в математическом кружке, Боря — в фотокружке, Витя — в авиамодельном кружке, Гриша — в шахматном кружке.

Самостоятельно сделайте вывод о том, кто из ребят в каком классе учится.

22.4. Использование таблиц истинности для решения логических задач

Аппарат алгебры логики позволяет применять к широкому классу логических задач универсальные методы, основанные на формализации условий задачи.

Одним из таких методов является построение таблицы истинности по условию задачи и её анализ. Для этого следует:

1) выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами;
2) записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций;
3) построить таблицу истинности для полученных логических выражений;
4) выбрать решение — набор логических переменных (элементарных высказываний), при котором значения логических выражений соответствуют условиям задачи;
5) убедиться, что полученное решение удовлетворяет всем условиям задачи.

Пример 6. Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:

1) если А получит максимальную прибыль, то максимальную прибыль получат B и С;
2) А и С получат или не получат максимальную прибыль одновременно;
3) необходимым условием получения максимальной прибыли подразделением С является получение максимальной прибыли подразделением B.

По завершении года оказалось, что одно из трёх предположений ложно, а остальные два истинны.

Выясним, какие из названных подразделений получили максимальную прибыль.

Рассмотрим элементарные высказывания:

• А — «А получит максимальную прибыль»;
• В — «B получит максимальную прибыль»;
• С — «С получит максимальную прибыль».

Запишем на языке алгебры логики прогнозы, высказанные экономистами:

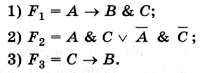
Составим таблицу истинности для F₁, F₂, F₃.

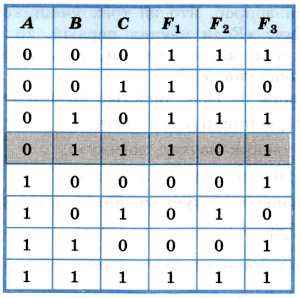
Теперь вспомним, что из трёх прогнозов F₁, F₂, F₃ один оказался ложным, а два других — истинными. Эта ситуация соответствует четвёртой строке таблицы.

Таким образом, максимальную прибыль получили подразделения В и С.

Cкачать материалы урока