Уроки 42 - 48
§2.8. Перевод чисел из одной системы счисления в другую

Содержание урока

2.8.1. Перевод целых чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

Вывод алгоритма перевода целых десятичных чисел в двоичную систему счисления

Алгоритм перевода целых десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления

Практическое задание «Перевод целого десятичного числа в целое двоичное, восьмеричное и шестнадцатеричное числа»

Перевод целого десятичного числа в целые двоичное, восьмеричное и шестнадцатеричное числа

Контрольные вопросы. Задания. Компьютерный практикум

2.8.2. Перевод дробей из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

2.8.3. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную и обратно

2.8.1. Перевод целых чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

Вывод алгоритма перевода целых десятичных чисел в двоичную систему счисления

Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере перевода чисел из десятичной системы в двоичную, при этом необходимо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут различаться.

Вывод алгоритма перевода целых десятичных чисел в двоичную систему счисления

Пусть А_цд — целое десятичное число, разложим его в ряд по основанию 2. Получим запись в развернутой форме двоичного целого числа, так как в этой записи будут отсутствовать отрицательные степени основания, т. е. числа 2:

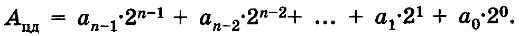
На первом шаге разделим число А_цд на основание двоичной системы, т. е. на 2. Частное от деления будет равно:

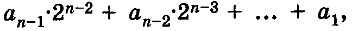
а остаток равен а₀.

На втором шаге целое частное опять разделим на 2, остаток от деления будет теперь равен a₁

Если продолжать этот процесс деления, то после n-го шага ползшим последовательность остатков:

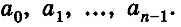
Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме:

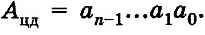
Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число.

Аналогичные рассуждения могут быть проведены и для перевода целых десятичных чисел в восьмеричную и шестнадцатеричную системы счисления.

Следующая страница Алгоритм перевода целых десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления

Cкачать материалы урока