Урок 15
Этапы моделирования
(§8. Этапы моделирования)
Содержание урока
Разработка модели
Разработка модели
На этапе разработки информационной модели нужно:
• определить исходные данные, существенные для решения данной задачи;
• выбрать тип модели;
• построить формальную модель, отражающую только существенные свойства оригинала;
• разработать алгоритм исследования формальной модели;
• построить компьютерную модель.
Существенные данные. В первую очередь нужно выяснить, что влияет на полёт шарика, а что — нет. Легко понять, что наличие кепки и её цвет, а также цвета мячика и мишени никак не влияют на результат, поэтому включать их в модель не нужно 1. Кроме того, для упрощения введём следующие допущения:
• мяч и мишень — материальные точки;
• мишень неподвижна;
• сопротивление воздуха не учитывается.
В другой ситуации они могут быть важны, например, когда Васю интересует в первую очередь свой внешний вид, а не попадание в мишень.
Выбор типа модели. При решении задачи могут использоваться несколько моделей разных типов. Например, для лучшего понимания полезно построить графическую модель задачи (рис. 2.12).
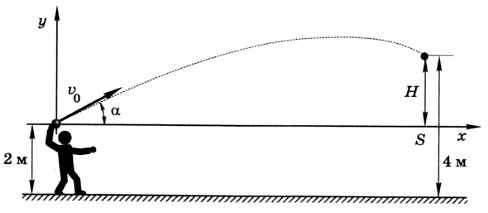
За начало координат удобно принять точку, откуда вылетает мяч. Обозначим через V0 начальную скорость мяча, через Н разницу высот (Н = 4-2 = 2 м), а через S — расстояние до мишени (S = 10 м). Однако графическая модель не даёт ответа на поставленный вопрос, поэтому для окончательных расчётов требуется построить математическую модель.
Формальная модель. В этой задаче формальная модель — это математическая модель движения тела, брошенного под углом к горизонту. Изменения координат описываются формулами:
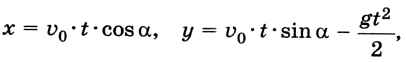
где q ≈ 9,81 м/с2 — ускорение свободного падения. Задача сводится к тому, чтобы найти два неизвестных, t и α, при которых х = S и у = Н, т. е.
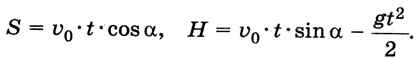
Эти формулы и представляют собой математическую модель задачи. В них нет упоминания о Васе, мяче, мишени и т. п., есть только условные обозначения и связывающие их формулы, это формальная модель, записанная на языке математических формул.
Алгоритм исследования модели. Алгоритм — это чётко определённый план действий, который приводит к решению задачи. В данном случае требуется разработать алгоритм использования модели: как с помощью полученных уравнений найти угол, под которым Васе нужно бросить мяч?
Например, можно постепенно увеличивать угол, начиная с нуля, и каждый раз строить всю траекторию полёта. Если при каком-то значении угла мяч пролетел ниже мишени, а при следующем — выше неё, дальше можно применить метод половинного деления для уточнения решения.
Но лучше поступить более грамотно, значительно сократив вычисления. Дело в том, что из первого уравнения S = v0 • t • cos а при известном значении угла а можно сразу найти время, за которое мяч пролетит расстояние до мишени. Тогда рассчитывать всю траекторию полёта не надо, остаётся только найти координату у и сравнить её с нужным значением Н. Таким образом, правильный выбор алгоритма может существенно влиять на вычислительную сложность моделирования, а иногда — и на результат.
Компьютерная модель. На этом этапе нужно выбрать средство моделирования и с его помощью построить компьютерную модель. Например, можно применить табличный процессор (OpenOffice.org Calc, Microsoft Excel и т. п.), написать собственную программу на одном из языков программирования или использовать готовую среду для моделирования (например, Simulink или VisSim).
Следующая страница 
Тестирование модели
Cкачать материалы урока
